类不平衡问题的Schur分解类重叠欠采样
点击数: 1019 更新日期: 2023-03-31
中文题目:类不平衡问题的Schur分解类重叠欠采样
论文题目:Class-overlap undersampling based on Schur decomposition for class-imbalance problems
录用期刊/会议:【Expert Systems With Applications】 (JCR Q1-Top)
原文DOI:https://doi.org/10.1016/j.eswa.2023.119735
原文链接:https://doi.org/10.1016/j.eswa.2023.119735
录用/见刊时间:2023.2.21
封面图片:
封面摘要:
作者列表:
1) 代琪 中国石油大学(北京)信息科学与工程学院 控制科学与工程 博20
2) 刘建伟 中国石油大学(北京)信息科学与工程学院 自动化系 教师
3) 施永辉 华北理工大学 理学院 网络空间安全
文章简介:
对于类不平衡问题,很多研究者认为类分布不平衡并非影响分类模型性能的主要因素,当类分布不平衡与类重叠、小间断和噪声等问题同时存在时,模型性能将受到严重的影响。现有的方法主要是在局部区域使用最近邻等方法获取样本的局部相似性,并发现数据集中的重叠区域。据我们所知,我们首次在类不平衡数据中使用矩阵分解方法处理类重叠问题。为了寻找数据集的全局相似性,提出一种新的Schur分解的类重叠欠采样方法(SDCU)。该方法试图在全局相似性上获取潜在的重叠样本。
对于类重叠问题,少数类样本附近的多数类样本是容易与少数类样本出现重叠的样本,因此,它们使用最近邻等方法获取少数类样本周围的样本。但是,这样的方式容易陷入局部最优的问题,因为当少数类过于靠近时,同一个多数类样本可能会成为其他少数类样本的最近邻,此时获取的重叠范围很小,甚至不能起到任何作用。如果少数类样本存在噪声时,这类方法很容易删除非重叠多数类样本。因此,我们受对比学习和度量学习的启发,首次将schur矩阵分解方法用于度量样本的全局惯性指数,提出一种新的欠采样方法。
SDCU是一种简单有效的欠采样方法,该方法使用欧氏距离和余弦相似度作为相似度度量方法。SDCU的计算过程主要分为四个阶段:相似矩阵计算、schur分解、样本选择与删除和新训练集生成。
阶段1:使用距离度量函数生成相似度矩阵
定义3 (欧氏距离) 如果![]()
和![]()
为数据集![]()
中的两个样本,则欧氏距离![]()
的定义如下:
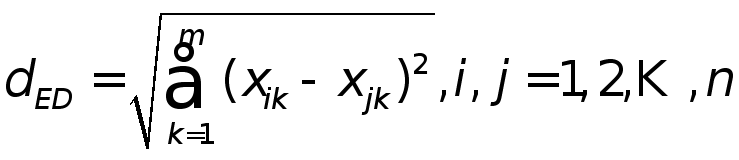
定义4 (余弦相似度) 给定数据集![]()
两个样本![]()
和![]()
,则余弦相似度![]()
的定义如下:
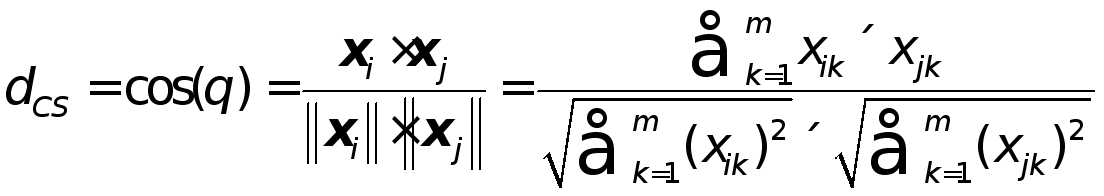
其中,![]()
。
阶段2:使用Schur矩阵分解方法分解全局相似度矩阵![]()
阶段3:多数类样本选择
在应用SDCU之前,这一步需要注意以下三点:
(1) 如果矩阵中样本对应的特征值为0,则该样本默认保留在数据集中,不做任何处理。
(2) 在我们的SDCU方法中,我们需要假设多数类和少数类样本集的惯性指数的正负是不同的,实验结果表明,该假设是可行的,但是,该假设尚未得到理论证实。此外,这也是未来可以研究的一个问题。
(3) 在删除过程中,可能会出现需要删除的样本数超过了两类样本数之差。对于这类情况,当需要删除正特征值的样本时,则按照从大到小的顺序删除多数类样本;直到少数类与多数类样本数相同时停止删除样本。反之,则按照从小到大的顺序依次删除多数类样本,直到两类样本数量相同,则停止删除。
阶段4:生成新的训练子集
限于篇幅原因,仅给出与其他先进模型的对比实验的部分结果。SDCU的全部实验及参数分析内容等具体内容请参考原文。图1显示了SDCU算法在KEEL数据库中ecoli2、new-thyroid1和yeast3三个数据集上的散点图(该图像是使用PCA处理后的二维图)。图1(a,c,e)为上述三个数据集使用余弦相似度构建相似矩阵的CSDCU欠采样方法的散点图,图1(b,d,f)为上述三个数据集为使用欧氏距离构建相似矩阵的ESDCU欠采样方法的散点图。其中红色的圆点表示少数类样本,蓝色的圆点表示多数类样本,而灰色的圆点表示使用SDCU欠采样删除的多数类样本。
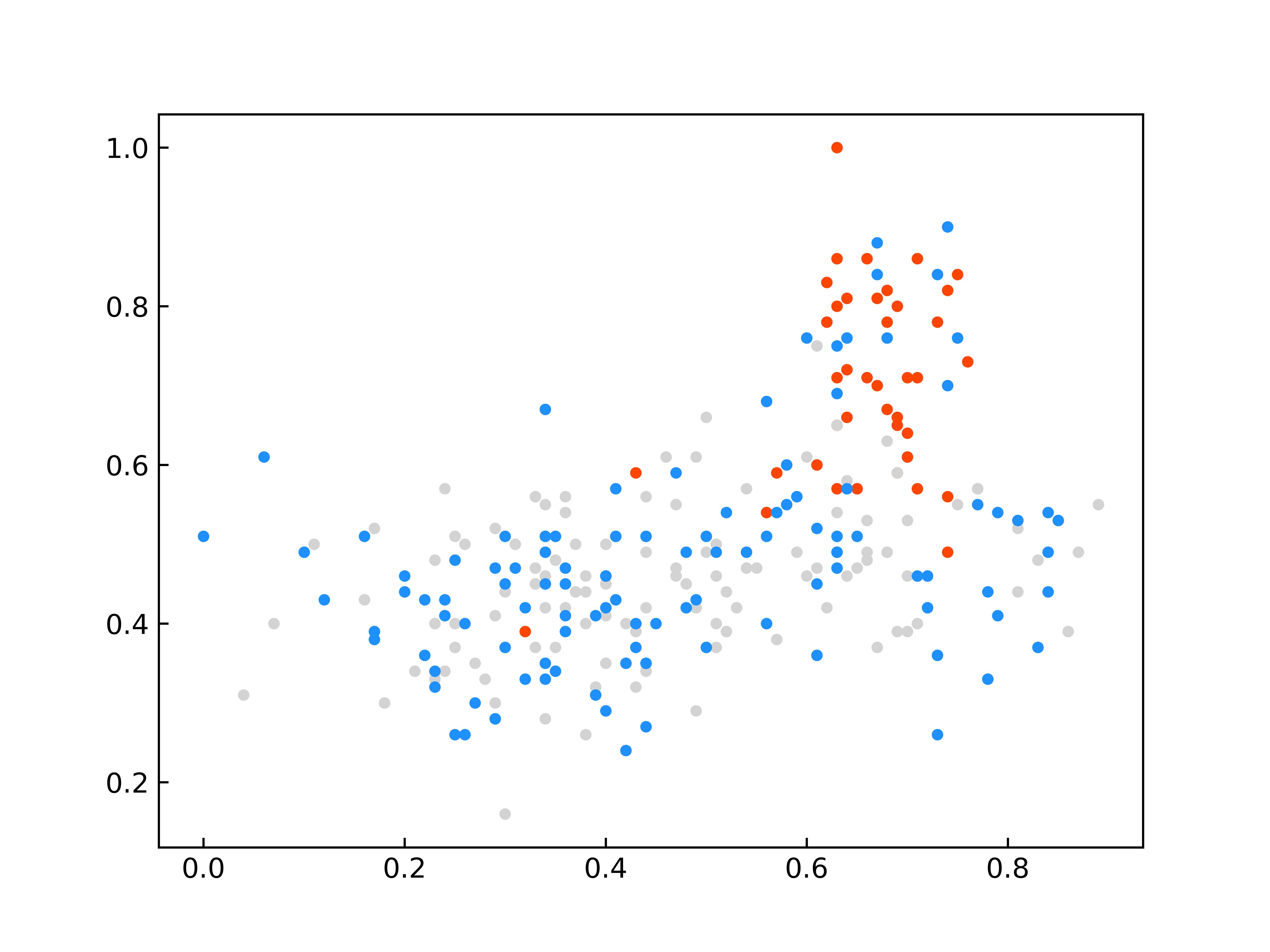
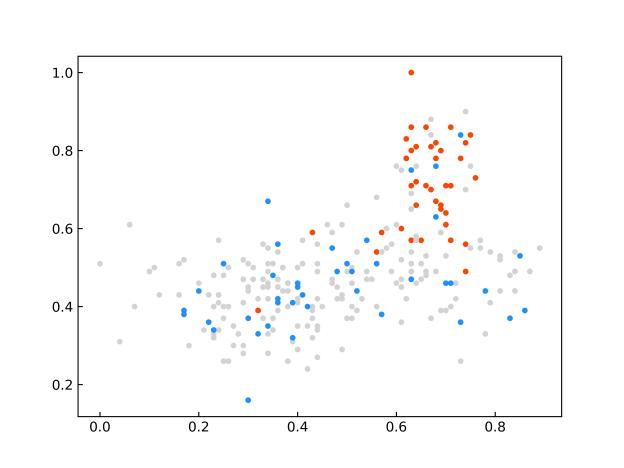
(a)ecoli2-CSDCU (b)ecoli2-ESDCU
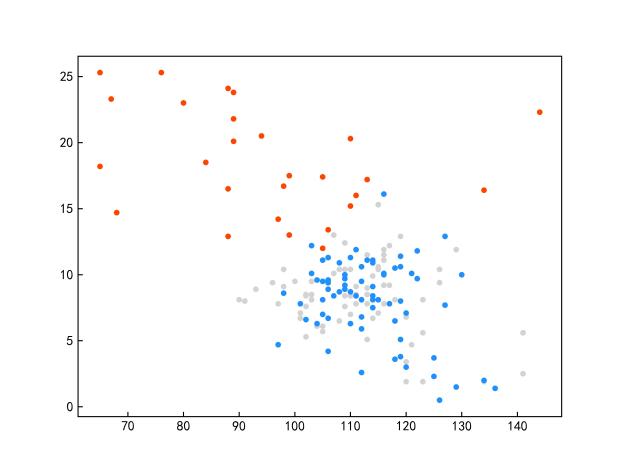
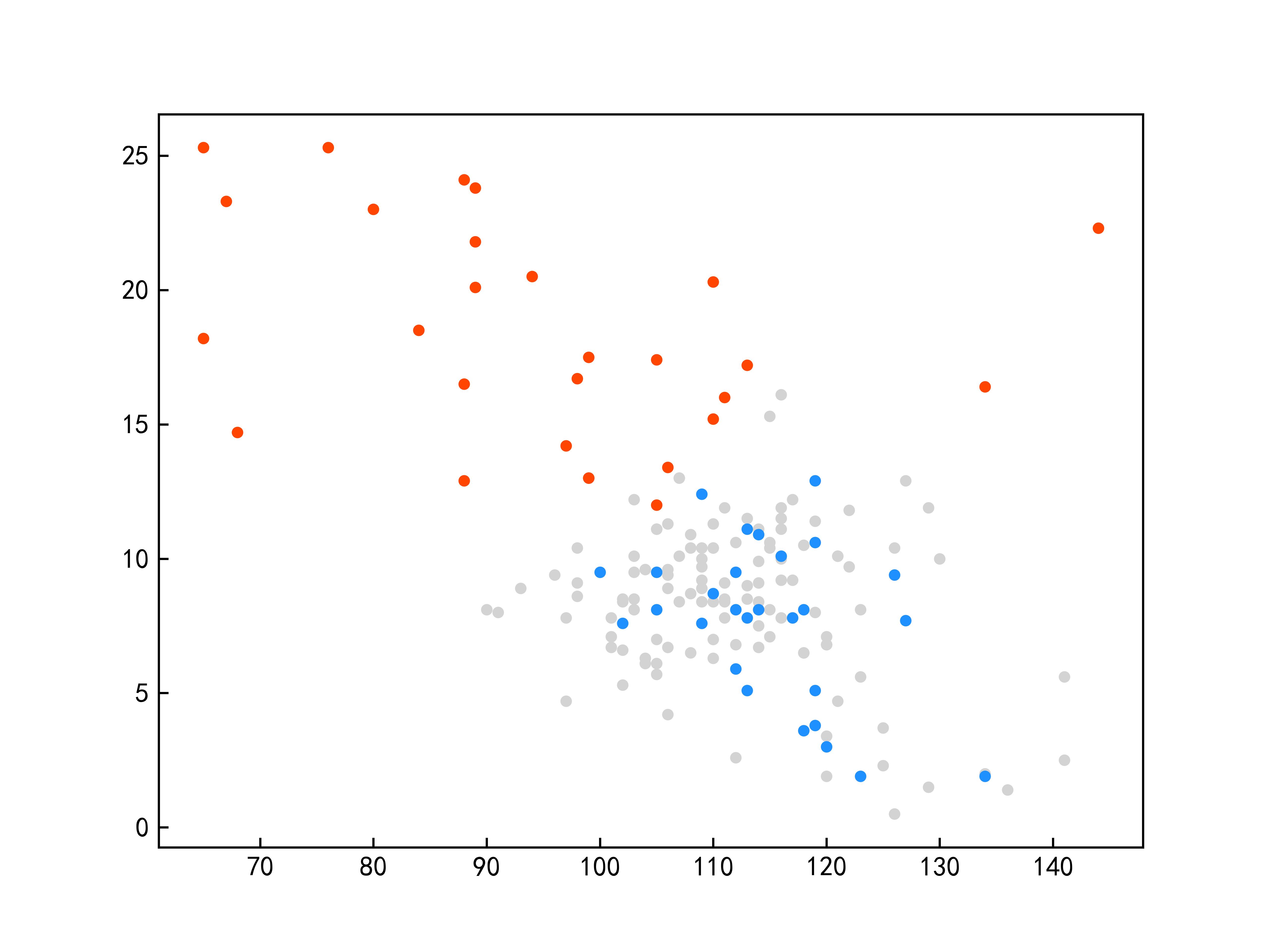
(c)new-thyroid1-CSDCU (d)new-thyroid1-ESDCU
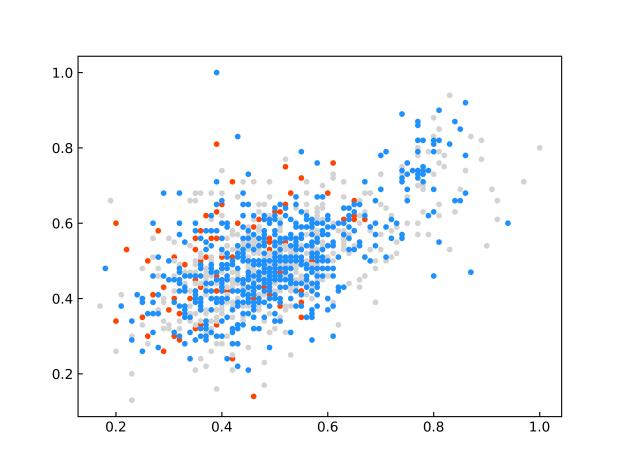
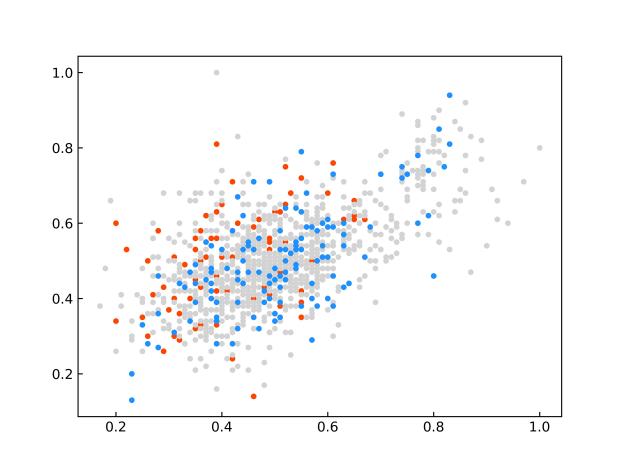
(e)yeast3-CSDCU (f)yeast3-ESDCU
图1 部分数据集上的散点图
接下来,介绍与其他先进方法的对比实验结果,如图2-4所示。另外,图5给出了所有模型的AUC均值。
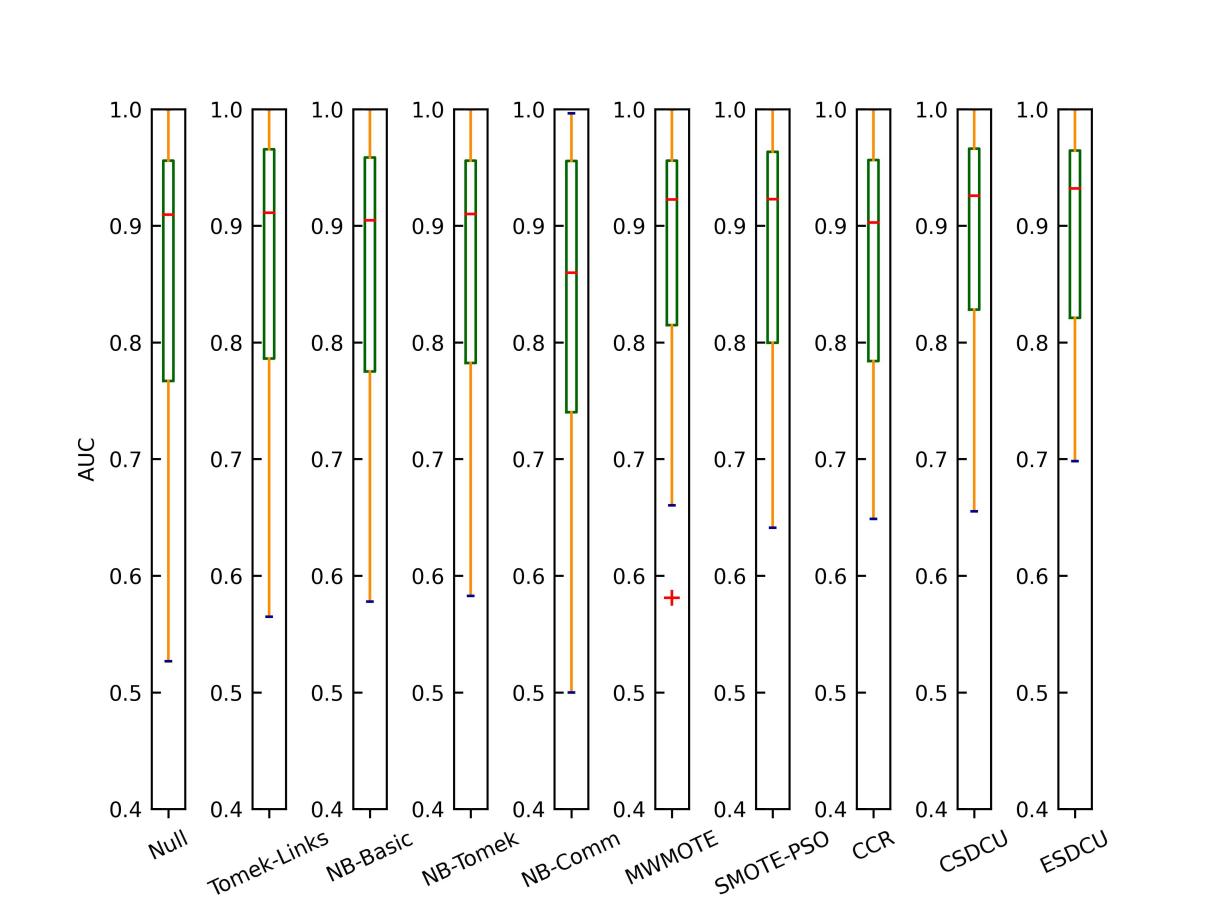
图2 不同重采样方法在所有数据集上的箱型图(SVM)
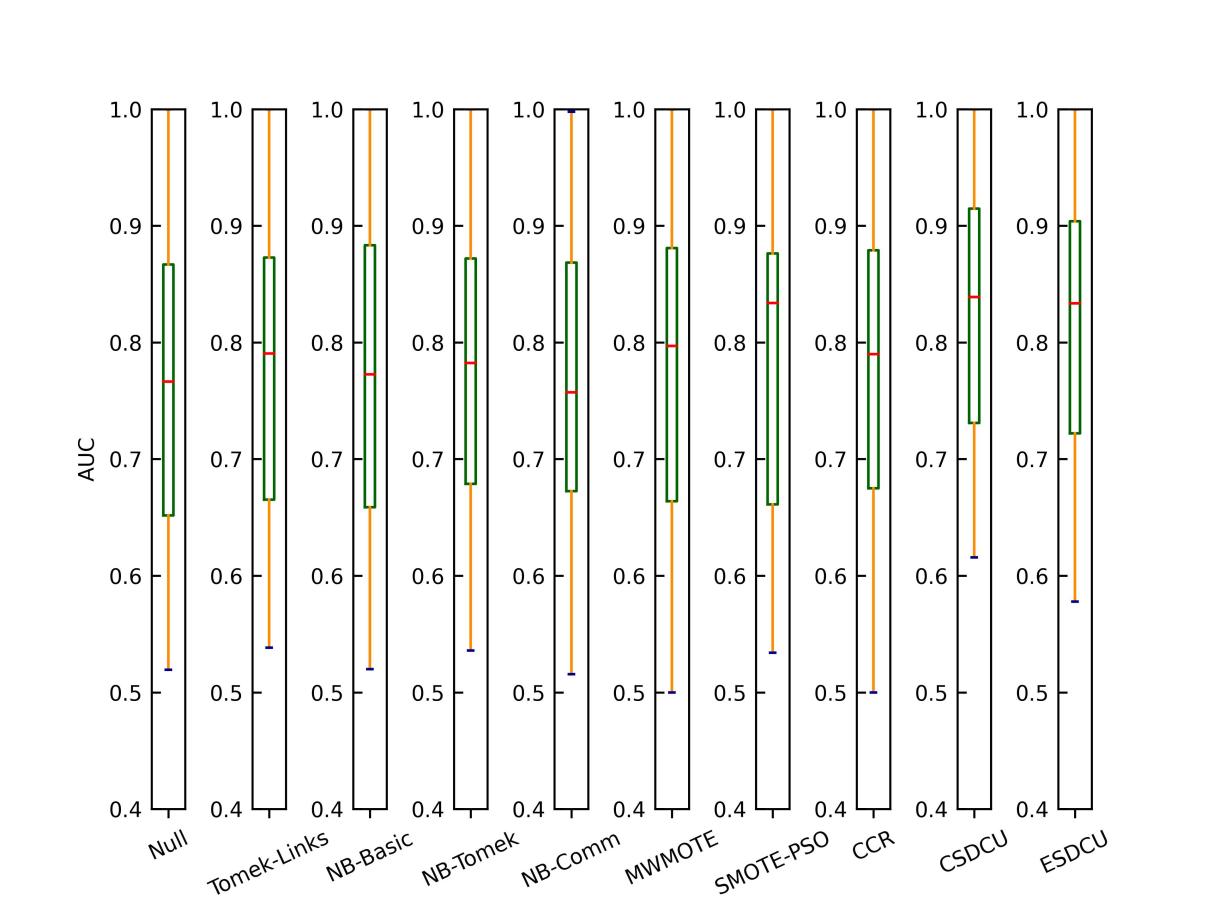
图3 不同重采样方法在所有数据集上的箱型图(CART)
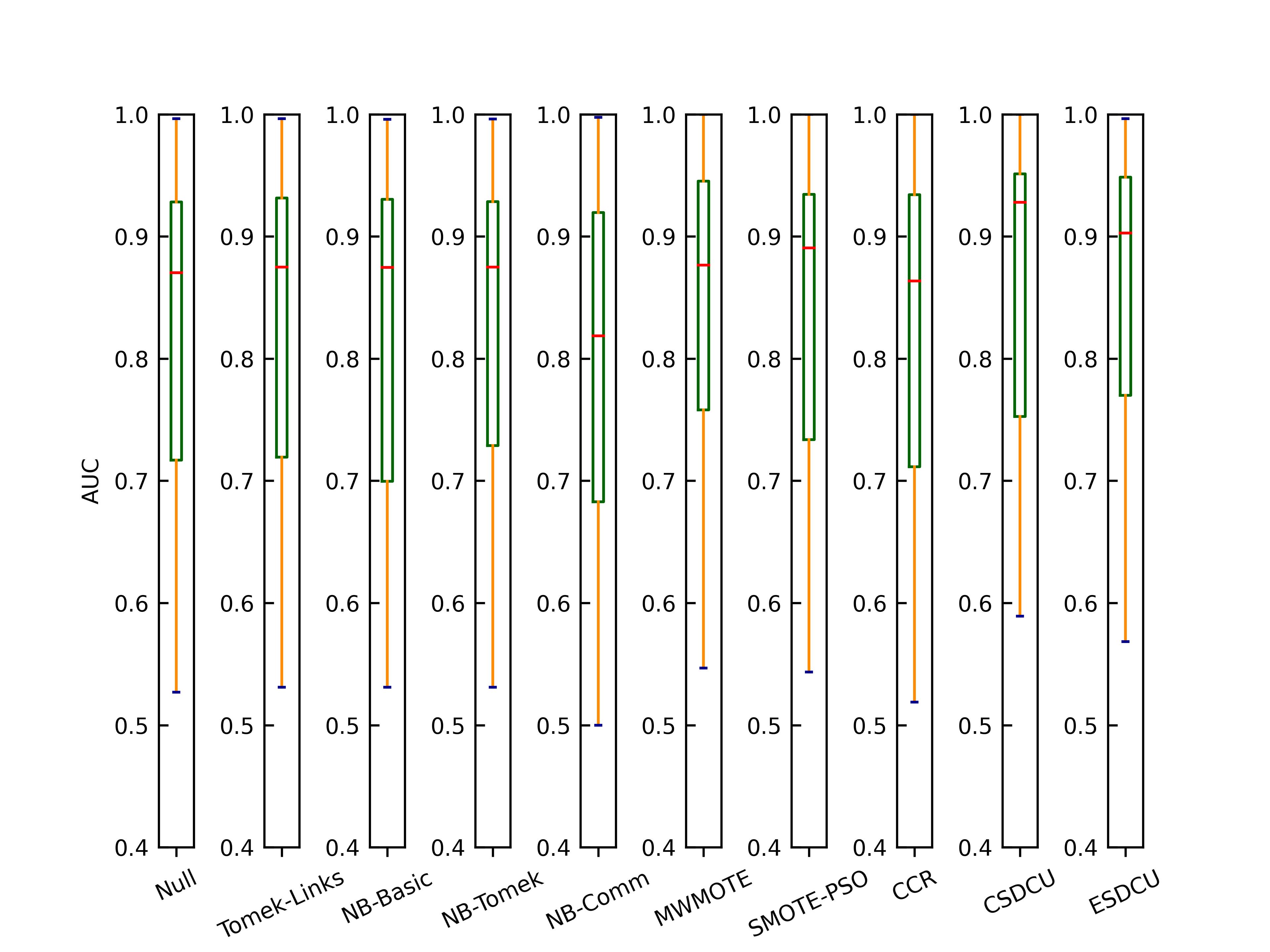
图4 不同重采样方法在所有数据集上的箱型图(3NN)
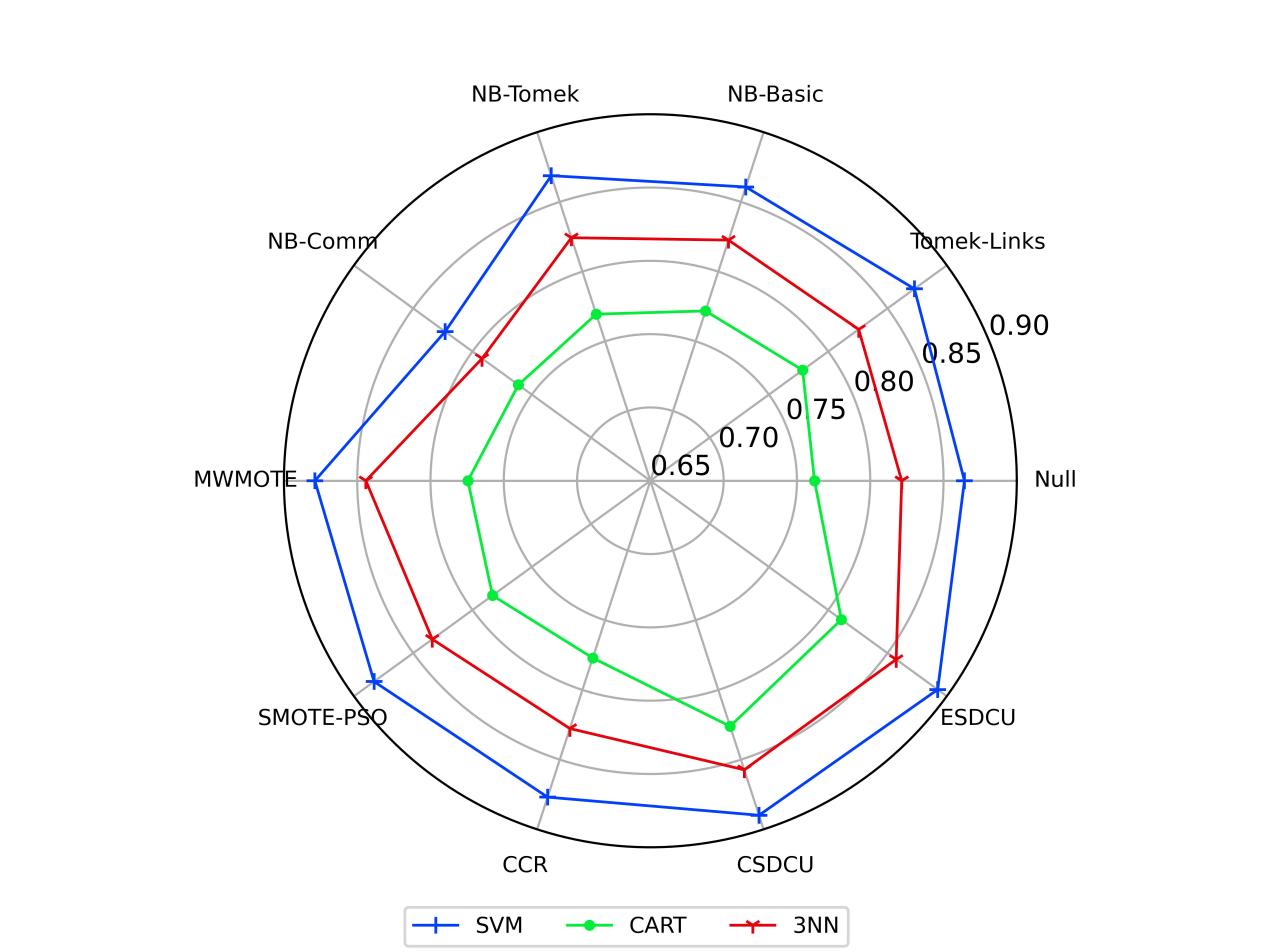
图5 所有数据集上对应方法的AUC均值
根据图5的结果我们可以观察到,SVM的性能是最好的,而3NN则是其次。由于CART和3NN是基于规则的分类器,因此,当我们删除多数类样本时,则很容易造成CART和3NN分类模型无法准确地学习多数类样本的分类规则,导致模型的分类性能降低。根据图2-4的粗略分析可以简单的得出结论,SDCU类的分类模型的性能是优于其他重采样技术的。
我们受对比学习和度量学习的启发,结合Schur矩阵分解方法,考虑全局相似度提出一种新的数据重采样方法,该方法首次尝试使用矩阵分解方法获取样本之间的全局相似度或样本的正负趋势。实验结果表明,SDCU与MWMOTE等重采样技术相比,SDCU具有明显的优势。当数据集中类不平衡问题更严重时,可以优先选择ESDCU。然而,对于类不平衡问题影响很小时,建议使用CSDCU,其性能更加优秀,且移除多数类样本更保守。
刘建伟 自动化系博士生导师/硕士生导师。长期从事模式识别与智能系统、复杂系统分析与智能控制、机器学习和数据挖掘方面的研究工作。在国际国内期刊上和国际国内会议上发表学术研究论文260多篇,其中三大检索200多篇。