中文题目：基于近似最小一乘的Hammerstein-Winner 时滞模型辨识

论文题目：Identification of Hammerstein-Wiener time delay model based on approximate least absolute deviation

录用期刊/会议：International Journal of Modelling, Identification and Control (EI)

录用/见刊时间：2022年06月

作者列表：

1） 徐宝昌 中国石油大学（北京）信息科学与工程学院/人工智能学院 自动化系教师

2） 荣志超 中国石油大学（北京）信息科学与工程学院/人工智能学院 硕18

3） 王雅欣 中国石油大学（北京）信息科学与工程学院/人工智能学院 博19

4） 袁力坤 中国石油大学（北京）信息科学与工程学院/人工智能学院 博17

文章简介:

日益复杂的实际生产过程中存在着大量非线性过程。Hammerstein-Wiener模型是一种典型的块连接模型，这种模型通过组合输入非线性模块、线性模块、输出非线性模块来近似描述实际生产过程。同时，很多情况下存在不符合正态分布的尖峰噪声和不确定的时滞。为了准确辨识出模型参数和时滞参数，提出了一种基于最小一乘准则函数的两步辨识算法。

设计与实现:

图1 Hammerstein-Wiener时滞模型结构图

同时进行时滞参数和模型参数的辨识是比较困难的，因此将时滞参数和模型参数分开进行估计，提出了基于近似最小一乘准则函数的两步法。这种方法的核心思想是模型参数和时滞参数分离开，进行交替估计。首先给定时滞参数一个初值，进行模型参数估计，然后根据模型参数估计时滞参数，直至模型参数和时滞参数都收敛至真值。仿真实验表明，目标函数采用最小一乘准则的两步法能够有效抵抗尖峰噪声的干扰，并且能够准确估计出模型参数和时滞参数；基于最小二乘的辨识算法受到尖峰噪声影响较大，甚至无法进行辨识。

实验结果:

pH中和系统如图2所示，代表容器容积，其中浓度为0.02mol/L的醋酸作为输入流在连续搅拌釜反应器中通过浓度为0.5mol/L氢氧化钠的滴定流进行滴定。滴定流分为和两部分，为恒定的，由计算机信号进行调节。该pH中和过程可近似建模为Hammerstein-Wiener模型。

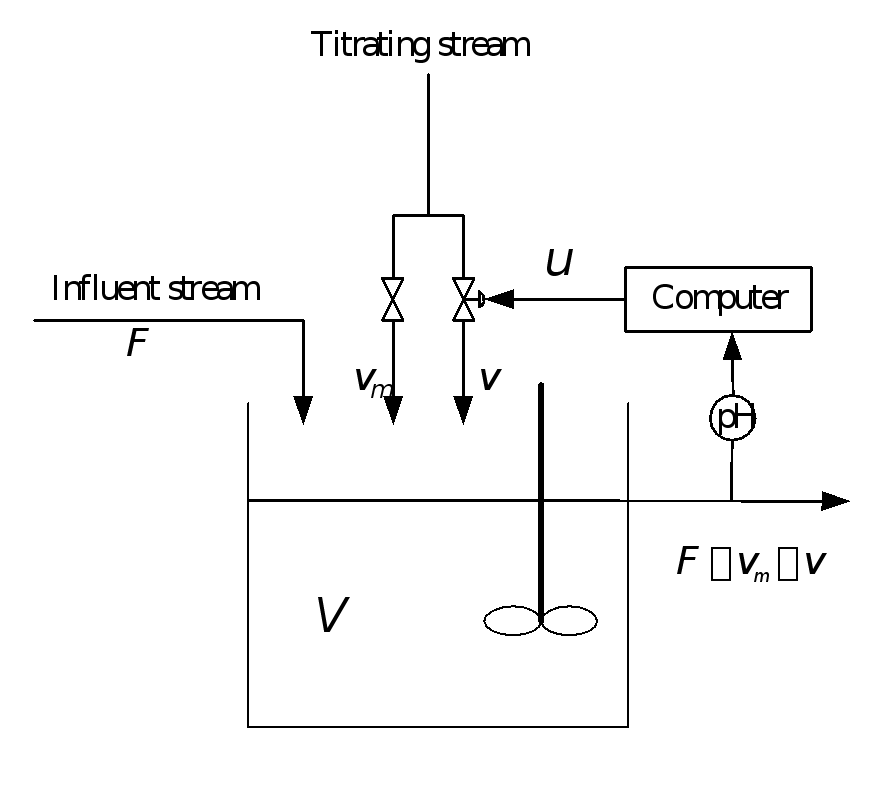
图2 pH中和过程流程图

当辨识过程中仅存在白噪声时，基于最小一乘准则函数的两步法（ALADSG）和基于最小二乘准则函数的两步法（LSSG）的辨识曲线和辨识结果如图3和表1所示。

图3 仅含白噪声时辨识曲线

表1 仅含白噪声时辨识结果

观察表1，可以看出两种算法都可以估计出模型参数和时滞参数，观察图3，可以看出基于最小二乘的两步法的相对误差曲线能够更快收敛，时滞参数能够更早的稳定。因此，当辨识过程中仅存在白噪声时，采用基于最小二乘的两步法效率更高，符合以往的研究。

当辨识过程中存在概率为5%，幅值为白噪声序列5倍的尖峰序列噪声时，两种算法的辨识曲线和辨识结果如图4和表2所示。

图4 =5%，A=5时辨识曲线

表2 =5%，A=5时辨识结果

根据表2可知，加入概率为5%，幅值为白噪声序列5倍的尖峰序列噪声后，最小二乘两步法受到影响更大，辨识精度大幅下降；而最小一乘两步法仍然能够保持较高精度进行辨识。根据图4可知，相比于仅含白噪声，引入尖峰噪声后，最小二乘两步法相对误差曲线波动变大，而最小一乘两步法基本没有变化。因此，当加入尖峰噪声后，采用最小一乘两步法辨识Hammerstein-Wiener模型优于最小二乘两步法。

为了进一步验证算法的鲁棒性，加入概率为10%，幅值为白噪声序列10倍的尖峰序列噪声。两种算法的辨识曲线和辨识结果如图5和表3所示。

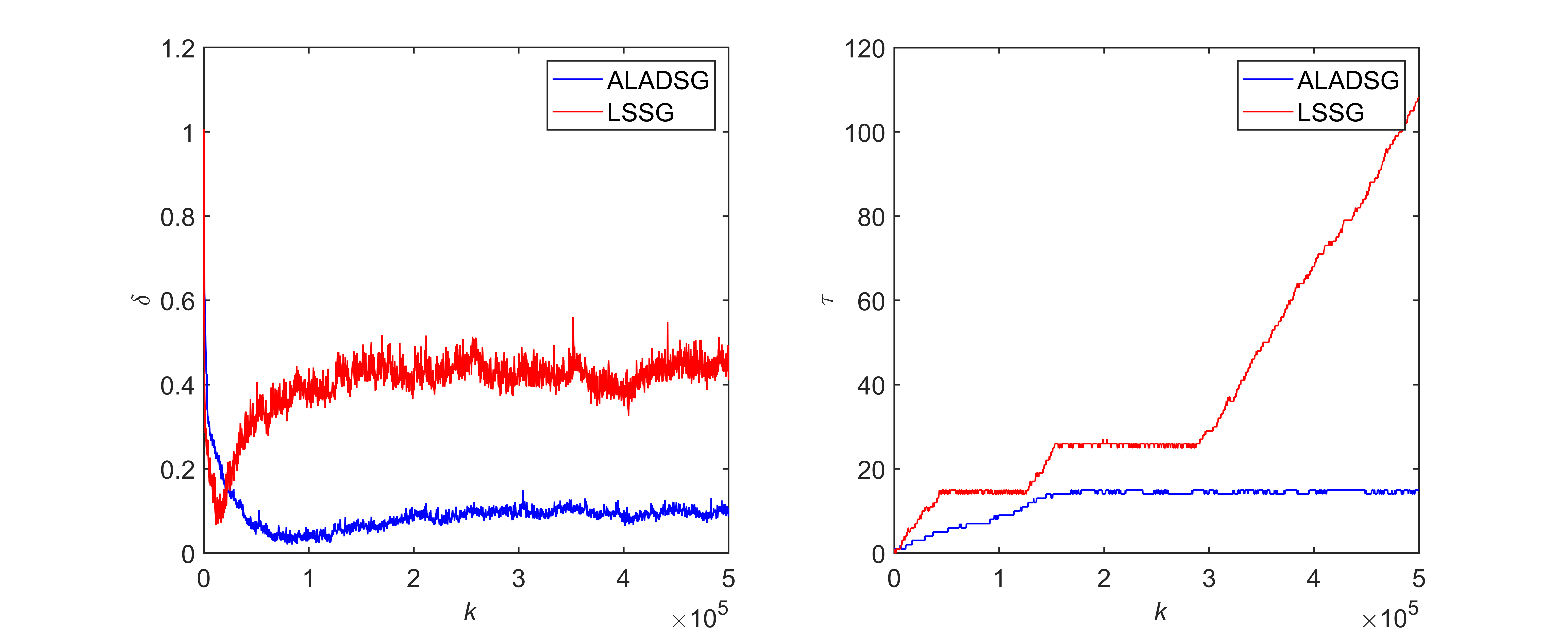
图5 =10%，A=10时辨识曲线

表3 =10%，A=10时辨识结果

观察表3和图5可知，加入概率为10%，幅值为白噪声序列10倍的尖峰序列噪声后，最小二乘两步法已经不能准确辨识模型参数，并且时滞参数也不能进行估计；最小一乘两步法仍能较为准确的辨识模型参数，并且能够准确估计出时滞参数，进一步验证了最小一乘两步法的鲁棒性。

作者简介:

徐宝昌，副教授，博士生导师，长期从事复杂系统的建模与先进控制；钻井过程自动控制技术；井下信号的测量与处理；多传感器信息融合与软测量技术等方面的研究工作。现为中国石油学会会员，中国化工学会信息技术应用专业委员会委员。曾参与多项国家级、省部级科研课题的科研工作，并在国内外核心刊物发表了论文60余篇；其中被SCI、EI、ISTP收录20余篇。