中文题目：基于LMI的混杂参数系统动态优化解的状态反馈实现方法：以催化裂化装置为例

论文题目：基于LMI的混杂参数系统动态优化解的状态反馈实现方法：以催化裂化装置为例

录用期刊/会议：中国过程控制会议（CAA A类会议）

作者列表：

1） 汪晓苏 中国石油大学（北京）人工智能学院 控制科学与工程 研22

2） 林嘉奖 中国石油大学（北京）人工智能学院 自动化系 教师

3） 罗雄麟 中国石油大学（北京）人工智能学院 自动化系 教师

3） 许 锋 中国石油大学（北京）人工智能学院 自动化系 教师

摘要:

混杂参数系统动态优化问题的间歇操作解常直接应用，然后再对连续操作解闭环化，这样难以体现间歇操作对闭环控制的影响。本文先线性化混杂系统，再将动态优化闭环问题转为跟踪问题，并设计基于LMI的迭代算法求解。最后以催化裂化装置为例验证方法的可行性。

背景与动机:

针对混杂参数系统动态优化问题，传统的解决方法是将间歇操作解直接应用，然后在对连续操作解闭环化，但这种方法无法体现间歇操作对闭环控制系统性能的影响。为了解决这一问题，首先对混杂参数系统线性化，然后通过求解混杂线性二次型调节器问题，进一步优化间歇操作对控制系统性能的影响，以实现更精确的控制和经济效益最大化。

设计与实现:

本文首先介绍了混杂参数系统的动态优化问题的形式以及解法。然后说明了如何得到混杂参数系统的HLQR问题，以及如何将动态优化开环最优解的实现问题转化为HLQR问题，最后给出了HLQR问题的迭代LMI形式的解法。最后，以带CO助燃剂的催化裂化装置为例，说明了如何将本文的算法用到实际的工程问题中。

（1）混杂参数系统的动态优化问题

混杂参数系统指同时包含连续操作和间歇操作的系统。在数学上可以直接将间歇操作建模为微分、代数方程的参数，具体可以写为：

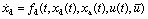
（2）线性混杂参数系统的HLQR问题

线性混杂参数系统是一种最简单的混杂参数系统，其中间歇操作在系统模型中以“线性”形式存在，具体可写为：

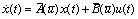
与LQR问题类似，HLQR问题的目标函数也包含关于和的二次函数的积分项。由于HLQR问题多了间歇操作，因此HLQR问题的目标函数还需要添加一项关于的二次项，即

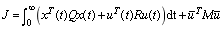
  （3）动态优化问题最优解的闭环实现

通过将动态优化问题的开环最优解当成目标轨迹，可以将混杂参数系统动态优化问题最优解的闭环实现转化为HLQR问题，此时可以进一步考虑间歇操作对系统控制性能的影响。

（4）HLQR问题的LMI解法

LQR问题的LMI形式可以由其对应的H2控制问题得到。与之类似，可以得到HLQR问题的BMI形式,在经过两次Finsler’s引理松弛后得到：

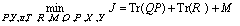
s.t.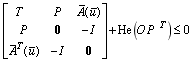

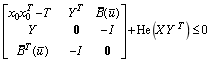
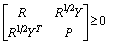
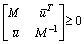
下面给出了具体的算法流程。

实验结果及分析:

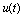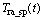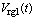      针对催化裂化装置，对其线性化和降阶后，将动态优化的连续操作变量选为反应温度的设定值和主风流量，间歇操作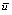选为CO助燃剂的添加量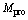。下面给出了算法的迭代过程和实验结果。

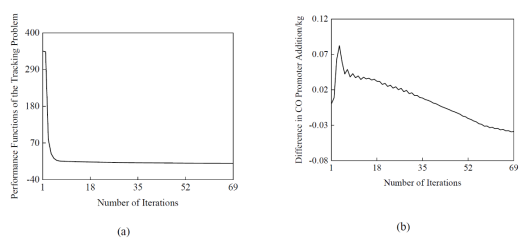
图1 算法1的迭代过程：(a)跟踪问题的性能函数；(b)CO助燃剂的差值

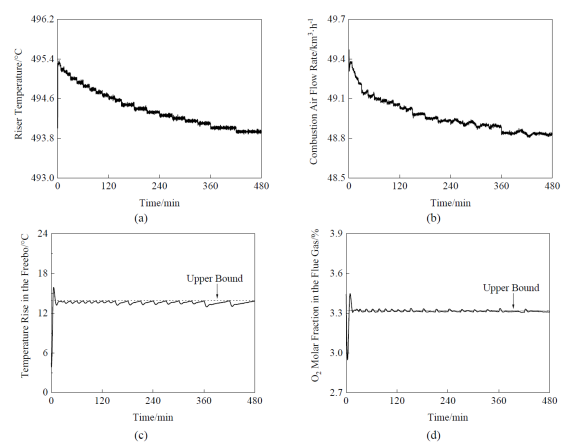
图3 干扰下的开环解状态反馈实现：(a)提升管反应温度；(b)主风流量；(c)稀相段温升；(d)烟气氧气含量

结论:

本文探讨了混杂参数系统动态优化问题中开环最优解的闭环实现。这通常指连续操作最优解的闭环实现，而间歇操作最优解则直接应用。在化工系统中，动态优化目标多为经济指标，常独立实现间歇与连续操作，却忽视了间歇操作对系统控制性能的影响。因此，最佳方法是在设计控制系统时纳入间歇操作的影响。本文先线性化混杂参数系统，再将闭环实现问题转化为HLQR问题，即BMI问题，需迭代算法转为LMI问题求解，保证目标函数单调不增。以催化裂化装置为例，说明HLQR构造方法。计算结果显示，CO助燃剂添加量增多会加剧系统动态变化，不利于控制，故间歇操作实现应略小于最优解。

通讯作者简介:

林嘉奖于2020年毕业于中国石油大学（北京）获控制科学与工程博士学位。目前就职于中国石油大学（北京）自动化系，助理教授。主要研究方向包括鲁棒控制，自适应动态规划，最优控制，混杂参数系统及其在化工过程等中的应用。