中文题目：MASC: 一种通过新颖的时空预测实现压缩的内存高效伴随灵敏度分析

论文题目：MASC: A Memory-Efficient Adjoint Sensitivity Analysis through Compression Using Novel Spatiotemporal Prediction

录用会议：61st ACM/IEEE Design Automation Conference (DAC '24)（CCF A）

录用时间：2024-2-27

原文DOI：https://doi.org/10.1145/3649329.3657393

作者列表：

1） 李晨曦 中国石油大学（北京）人工智能学院  硕 22

2） 张博源 美国印第安纳大学

3） 段永强 中国石油大学（北京）人工智能学院  硕 23

4） 李   阳 中国石油大学（北京）人工智能学院  硕 23

5） 叶佐昌 清华大学

6） 刘伟峰 中国石油大学（北京）人工智能学院 计算机系教师

7） 陶鼎文 美国印第安纳大学

8） 金   洲 中国石油大学（北京）人工智能学院 计算机系教师

背景与动机:

在现代集成电路设计和验证中，伴随灵敏度分析至关重要，但随着电路规模、目标函数数量以及时间点的增加，其计算开销会显著增长，这会妨碍其更广泛的应用。由于瞬态分析的前向积分过程和伴随灵敏度分析的反向积分过程具有密切的联系，所以我们可以保存瞬态分析中的雅可比矩阵，用于加速伴随灵敏度分析。然而，跨多个时间步长的雅可比矩阵组成的稀疏张量通常非常庞大，无法在正向积分过程存储在内存中，假如把这些数据存储在磁盘中又会带来显著的磁盘读写开销。为了解决这个问题，我们设计了一种内存开销极低的灵敏度分析方法，利用数据压缩来最小化仿真过程中的内存开销，并提高伴随灵敏度分析的效率。我们的压缩算法可以充分利用数据的电路特性和时空特性，可以高效压缩由雅可比矩阵组成的稀疏张量，还引入了共享索引技术、先进的时空预测模型和健壮的残差编码方案。最后我们在来自真实世界的7个数据集上评估了我们的压缩算法。与通用压缩算法相比，所提压缩算法的压缩率大约是GZIP的4倍，同时压缩时间是其25%；与浮点数压缩算法相比，所提算法压缩率大约是FPZIP的2.24倍、NDZIP的15.69倍以及SpiceMate的4.95倍，同时压缩时间大约是NDZIP的50%和SpiceMate的45%，稍慢于FPZIP。

设计与实现:

 （1） 高效的稀疏张量压缩算法

l共享索引以及时空预测技术

 

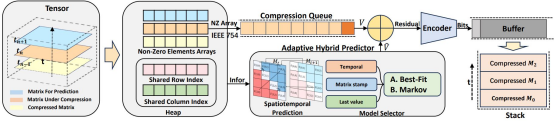
图 1 MASC压缩算法工作流程

上图描述了所提压缩算法中的原理和工作流程。为了有效的压缩雅可比矩阵构成的稀疏张量，我们首先以CSR等格式来存储稀疏矩阵，分别讨论对矩阵索引和非零元数组的压缩。

由于在同一次瞬态分析中雅可比矩阵的索引数组都是相同的，所以我们可以将索引数组仅仅保留一份，即在堆中保存一份共享索引，这些索引数组可以用整数压缩算法进一步的压缩。

由于非零元数组通常由IEEE 754浮点数组成，所以我们采用浮点数压缩算法进行高效的压缩。同时我们利用了时间上相邻雅可比矩阵之间的时间相关，以及由于器件Matrix Stamping过程所导致的数据空间相关性，构建了时空预测模型，高效的去除数据之间的冗余。

通过对整数索引的压缩以及浮点数非零元的压缩，我们有效的降低了仿真过程中的内存开销。

l预测模型选择

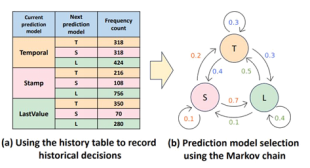
图 2 预测模型选择

为了减少选择最佳预测模型所带来的时间开销以及记录模型选择的空间开销，我们创新性地采用了马尔可夫模型。首先我们在压缩任务的开始阶段，对每种预测模型的精度进行判断，并选择精度最高的作为最终的预测模型，同时对预测模型的选择频率进行记录。在之后的压缩任务中，我们以频率估计概率，直接对预测模型进行选择，从而减少了开销。

l高效的残差编码方案

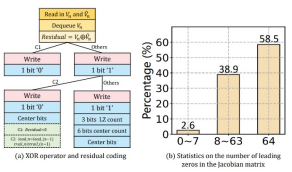
图 3 残差编码算法

压缩器从压缩队列的前端读取实际值，从混合预测器读取预测值，在它们之间执行异或操作以生成残差，之后编码器对这些残差进行编码。由于实际值和预测值通常非常接近，所以残差通常包含许多前导零和尾随零。因此，有效地编码这些零比特可以对浮点数进行有效的压缩。如上图所示，我们根据残差的数据特征采用了一套高效的残差编码方案，由于接近60%的残差的所有位为‘0’，所以我们采用1bit去编码这种情况，同时还采用了共享编码的方法去进一步提高压缩率。

lMASC工作流程

图 4 MASC仿真工作流程

完整的仿真工作流程如上图所示。在瞬态分析中，进行数据的压缩和存储。首先我们在计算电路的直流工作点时获得共享索引。在瞬态仿真中，MASC将tn时间点的雅可比矩阵存储到tn+1时间点，利用tn+1时间点获得的雅可比矩阵完成对tn时间点雅可比矩阵的压缩。同理，在灵敏度仿真过程中，整个过程逆向进行，完成对雅可比矩阵的解压与内存释放。

实验结果及分析:

表 1 压缩算法性能对比

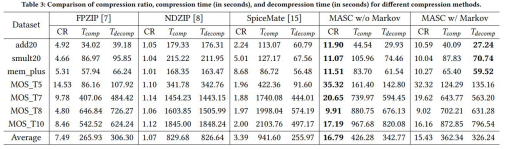
如上图所示，我们在多个电路上将所提时空压缩算法和浮点数压缩算法FPZIP，NDZIP，和 SpiceMate进行了性能比较，这些压缩算法分别来自高性能计算和电路仿真等多个领域。实验结果表明，时空压缩算法在压缩率、压缩时间和解压时间上都有着很好的表现。它的平均压缩率大约是FPZIP的2.24倍、NDZIP的15.69倍以及SpiceMate的4.95倍；其压缩时间大约是NDZIP的50%和SpiceMate的45%，稍慢于FPZIP。 最后，我们将压缩算法集成至电路仿真器xyce，与原本的xyce灵敏度仿真相比，时间开销减少了50%左右，这证明了我们所提仿真性能的优越性。

结论:

在本文中，我们将数据压缩算法集成到仿真过程中，利用前向积分过程中存储的雅可比矩阵来加速反向伴随灵敏度求解过程。同时，我们开发了一种新颖的无损压缩算法，可以大幅度的减少仿真过程中的内存开销。与通用压缩算法GZIP和最先进的浮点压缩算法FPZIP、NDZIP以及SpiceMate相比，所提压缩算法表现出显著的优势，有效地减少了伴随灵敏度仿真过程中的内存开销。

通讯作者简介:

金洲，副教授。中国石油大学（北京）计算机系副教授，入选北京市科协青年人才托举工程、校青年拔尖人才。主要从事集成电路设计自动化（EDA）领域工作的研究龙其是AI和 GPU加速的电路仿真等方向。主持并参与国家自然科学基金青年项目、重点项目，科技部重点研发微纳电子专项、高性能计算专项青年科学家项目，国家重点实验室开放课题，企业横向课题等。在DAC、TCAD、SC、PPoPP、ICCAD、DATE、IPDPS、TODAES 、TCAS-II等重要国际会议和期刊上发表60余篇高水平学术论文。获SC23最佳论文奖、EDA2青年科技奖、ISEDA23荣誉论文奖、IEEJ九州支部长奖等。 

联系方式：jinzhou@cup.edu.cn