中文题目：MSH：一种用于非线性直流仿真的高阻节点感知的多阶段同伦方法

论文题目：MSH: A Multi-Stage HiZ-Aware Homotopy Framework for Nonlinear DC Analysis

录用期刊/会议：2024 Design, Automation and Test in Europe Conference (DATE) (CCF-B类会议)

原文链接：https://ieeexplore.ieee.org/document/10546783

录用/见刊时间：2024-3-25

作者列表：

1）金   洲 中国石油大学（北京）人工智能学院 计算机系教师

2）冯   田 成都华大九天科技有限公司

3）吴   枭 北京华大九天科技股份有限公司

4）牛   丹 东南大学 自动化学院

5）周振亚 北京华大九天科技股份有限公司

6）卓   成 浙江大学 信息科学与电子工程学院

 

背景与动机:

非线性直流分析是晶体管级电路仿真中最重要的任务之一。同伦法在改善牛顿-拉夫逊（NR）方法的收敛性问题方面取得了巨大成功。然而，在某些高阻（HiZ）节点处嵌入同伦参数可能会导致该类节点在同伦参数达到1时的节点电压远离真实的直流解，即使理论上此刻的电路应该等价于原始电路，从而导致在最终的NR验证阶段出现新的收敛失败问题。在本文中，我们提出了一种HiZ节点感知的多阶段同伦框架MSH，使HiZ节点和其他节点能够分别进行多阶段延拓，以增强仿真的收敛性。

设计与实现:

（1）特定 HiZ 节点引起的 DC 收敛失败现象

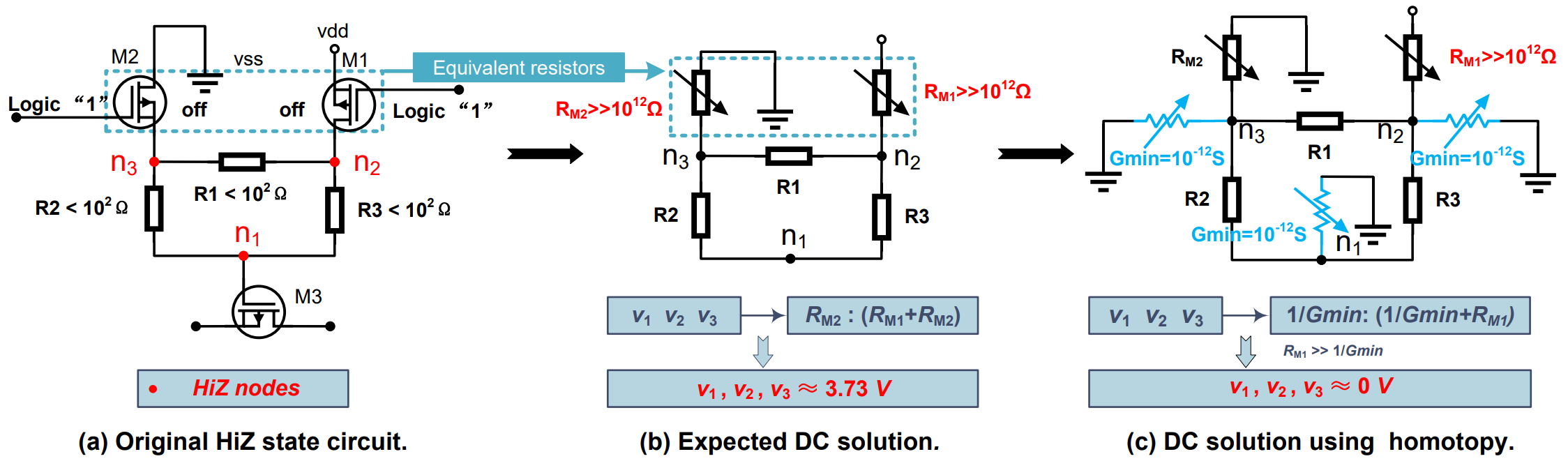
图1：同伦算法中由特定 HiZ 节点引起的 DC 收敛失败示意图

如图所示，当节点 n1~n3 呈高阻态时，晶体管M1和M2可以等效为两个无穷大的电阻。此时，节点 n1~n3的电压由RM2 与（RM1+RM2）的比值所决定，如图1（b），在该电路中，经计算可以得到 v1 = v2 = v3 ≈ 3.73 V。当使用同伦法对上述电路进行求解时，如图1（c）所示，节点 n1~n3的电压由1/Gmin与（1/Gmin+RM1）的比值所决定，由于 RM1（>>1e12 Ω）通常远远大于 1/Gmin（≈1e12 Ω），所以此刻有 v1 = v2 = v3 ≈ 0 V，这将会导致最终 NR 验证的失败。

（2）多阶段同伦框架

l多阶段-多参数同伦框架

该框架的同伦函数如下：

 

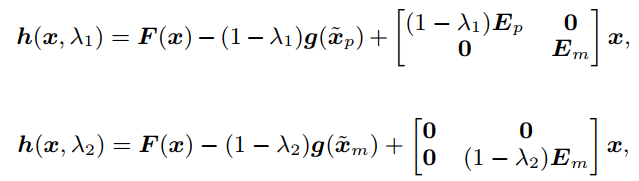
其中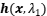， 为第一阶段的延拓方程，主要求解所有HiZ节点使其达到稳定状态。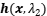为第二阶段的延拓方程，主要求解所有非HiZ节点。

lMOS可变增益同伦方程

为了进一步提升所提出的多参数-两阶段同伦算法在仿真MOS 电路时的效率，本文提出了一种 MOS 电流增益同伦方程（MCGH），以使得其解曲线更加平滑，从而实现快速 DC 仿真。如下公式所示，我们给MOS晶体管的漏源电流ids乘以了同伦参数λ，λ从0~1逐渐变化，以实现增益电流的连续变化。

 

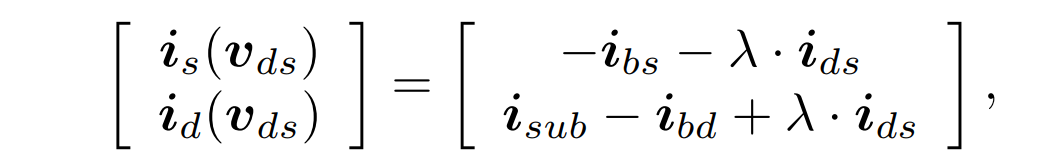
l弧长法追踪解曲线

同时，为了更好地保证收敛性，我们采取了弧长法对同伦方程的解曲线进行追踪。该方法主要分为预测和校正两个阶段。其预测阶段的需要求解的方程如下：

 

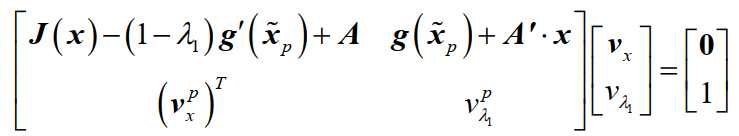
校正阶段的需要求解的方程如下：

 

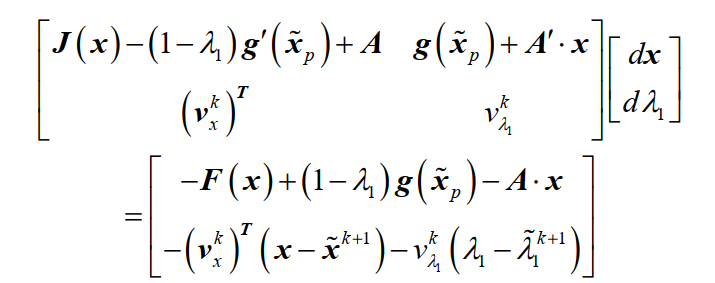
（3）HiZ节点的定位

本研究引入了一种简单而有效的技术来识别这类具有 DC 路径的 HiZ 节点。首先使用普通的 DC 算法对电路进行 DC 仿真。如果当右端项 RHS 足够接近 0 时出现了不收敛情况，首先检查每个不收敛节点的电流。如果节点电流小于给定阈值，则将该节点标记为 HiZ 节点。这样，该算法就可以在不引入额外开销的情况下，精确地定位具有 DC 路径的 HiZ 节点。

实验结果及分析:

（1）消除HiZ不收敛问题的有效性

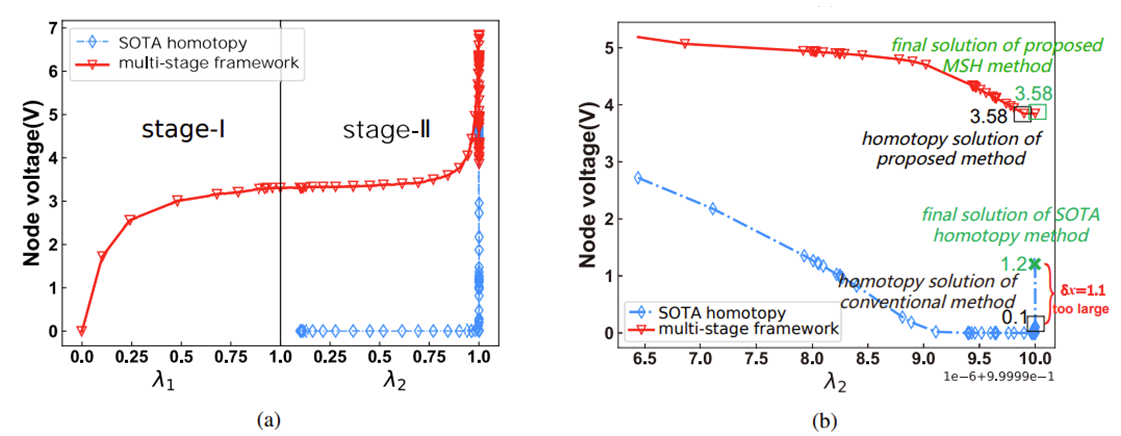
图2：(a)两种方法下HiZ节点的解曲线；(b) λ2非常接近1时的局部放大图

本文对一个工业 CMOS 电路进行了测试，该电路由 69334 个器件（包括 715 个 MOS 晶体管）组成，其具有16个HiZ节点。由图可知，SOTA同伦可以成功收敛，但在最终NR验证阶段不能收敛。MSH框架收敛成功。

（2）MOS可变增益同伦的收敛性

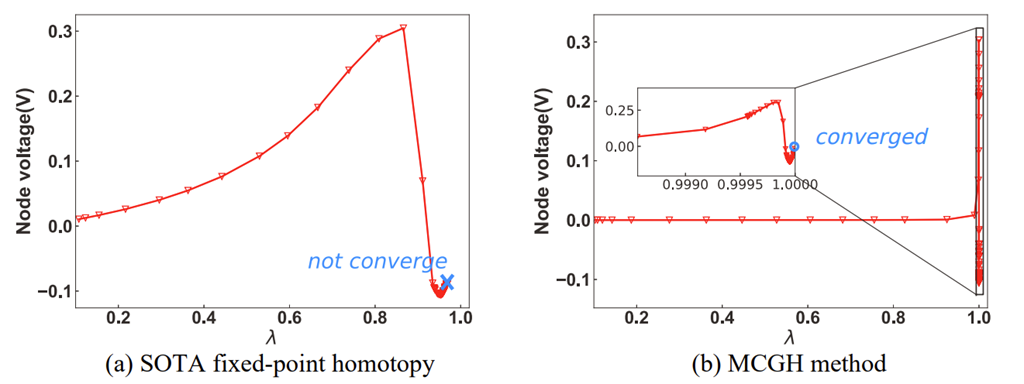
图3：两种同伦方法下MOSFET漏极节点的解曲线

由图可知，对于SOTA同伦，由于电流增益的强非线性，当λ达到0.96左右时，解曲线出现不连续。而本文所提出的MCGH可以收敛，并且λ最终迭代到1。此外，可以发现当λ在0~0.999之间时，我们方法的解曲线非常光滑，λ = 1附近的波动主要是由于我们引入的线性辅助算子所导致的。

（3）加速效率

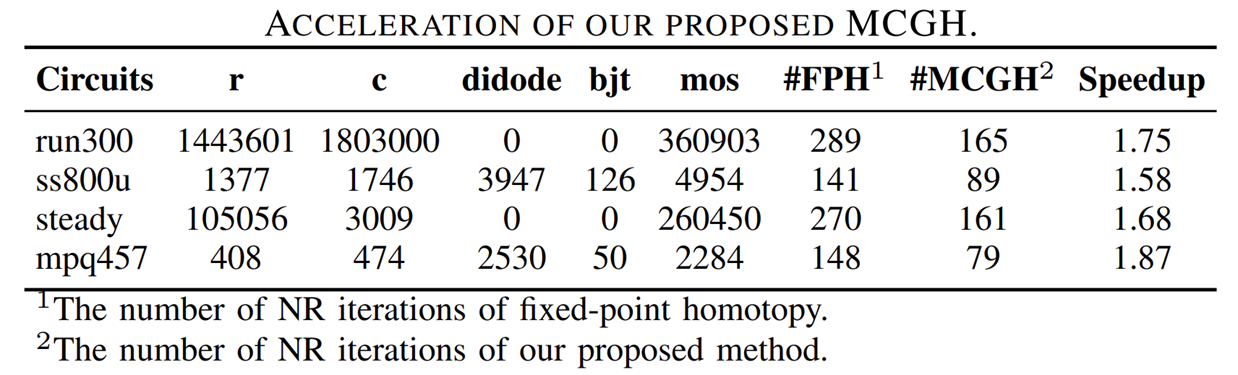
最后，基于本文所提出的 MSH 框架带来的收敛性提升，我们进一步评估了MCGH函数相比于SOTA同伦函数的加速效率。结果显示，基于MCGH函数的多阶段同伦框架相较于基于SOTA同伦函数的多阶段同伦框架大约平均加速了1.7倍。

结论:

本文提出了一种多参数同伦框架，可实现多阶段延拓，以解决非线性直流分析中特定HiZ节点引起的DC收敛失败问题。该框架采用全新的同伦函数实现快速延拓，采用弧长法对解曲线进行跟踪，保证了其收敛性。本文通过工业界大规模电路证明了我们框架的有效性，并且该框架相较于比SOTA不动点同伦实现了1.7倍的平均加速比。

通讯作者简介:

金洲，中国石油大学（北京）计算机系副教授，入选北京市科协青年人才托举工程、校青年拔尖人才。主要从事集成电路设计自动化（EDA）、面向科学计算的DSA软硬件协同设计等方面的研究工作。主持并参与国家自然科学基金青年项目、重点项目，科技部重点研发微纳电子专项、高性能计算专项青年科学家项目，国家重点实验室开放课题、企业横向课题等。在DAC、TCAD、TODAES、SC、PPoPP、IPDPS、TCAS-II、ASP-DAC等重要国际会议和期刊上发表60余篇高水平学术论文。获EDA2青年科技奖、SC23最佳论文奖、ISEDA23荣誉论文奖、IEEJ九州支部长奖等。

联系方式：jinzhou@cup.edu.cn