中文题目：EMGA: 一种用于MBIST内存分组的进化式算法

论文题目：EMGA: An Evolutionary Memory Grouping Algorithm for MBIST

录用期刊/会议：2024 International Symposium of Electronics Design Automation (ISEDA) (EI索引国际会议)

原文链接：https://www.ssslab.cn/assets/papers/2024-li-EMGA.pdf

DOI：10.1109/ISEDA62518.2024.10617612

录用/见刊时间：2024-3-26

作者列表：

1） 李阳 中国石油大学（北京）人工智能学院

2） 段永强 中国石油大学（北京）人工智能学院

3） 张昊 中国石油大学（北京）人工智能学院

4） 牛丹 东南大学 自动化学院

5） 吴枭 北京华大九天科技股份有限公司

6） 金洲 中国石油大学（北京）人工智能学院

 

背景与动机:

MBIST（存储器内置自测试）是芯片设计和制造中广泛使用的一种方法，用于检测和定位内存中的故障。由于现代芯片的存储器容量很大，因此需要对存储器进行分组，以便有效地进行管理和测试。传统的启发式算法在处理具有较多约束条件和存储器的MBIST分组问题时，往往面临时间复杂度高和分组结果质量较差的挑战。为了克服这些限制，本文提出了一种创新的基于启发式的MBIST分组算法。该算法通过优化启发式策略，不仅显著提高了求解效率，而且在保持高效率的同时实现了高质量的分组结果。

设计与实现:

（1）EMGA框架

 

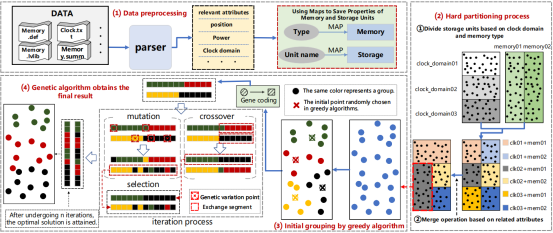
图1 总体EMGA算法实现流程

如图1所示，EMGA 包含三个主要部分。第一部分是解析器和硬分区。由于存储器类型、功耗和各种分组约束等属性信息几乎都存在于存储器的设计文件中，因此需要从文件中提取存储器信息和约束，并保存到相应的数据结构中。读取信息后，我们可以将约束分为硬约束和软约束。如图 3 所示，根据硬约束，对内存进行硬分区，得到初始分组。第二部分使用贪心算法来减少每个分组的大小，并根据初始分组快速获得满足硬约束和软约束的结果。第三部分使用遗传算法来寻找更少的分组，以避免局部最优解。

（2）约束条件

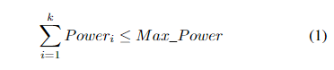
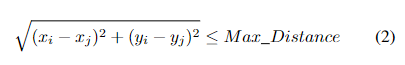
在分组过程中，首先要面对多约束问题。多约束指的是在分组过程中需要同时考虑各种因素或限制。如上述所示，我们选择了通常最重要的一些约束，（1）和（2）是功率约束和距离约束，（3）中的这些特性是必须满足的，如逻辑地址映射约束、时钟约束、类型约束、逻辑端口约束和写越界约束等。只有满足所有限制条件的存储器才能被分为一组，而且最终分组数量越少越好。

（3）贪心算法损失函数的定义

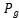是仅考虑功耗时的分组数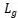，是仅考虑距离时的分组数，λ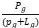为，μ为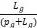。我们引入权重系数λ和μ，可以灵活地调整功耗和距离在损失函数中的重要性。这允许算法根据具体应用场景的需求，更侧重于功耗或距离的优化。Wi是将第 i 个内存添加到当前组后的功耗，Di是将第 i 个内存添加到当前组后的最大距离。Max_Power和Max_Distance是最大功耗和最大距离。我们将功耗和距离的变化除以它们的最大值，使得这两个量纲不同的指标具有可比性。这样，算法在每一步都可以公平地比较功耗和距离的影响。故损失函数F定义为：

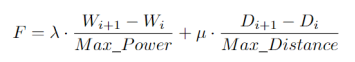
总的来说，这样的损失函数定义使得贪心算法能够在功耗和距离之间进行有效的权衡，从而在每一步都做出最优的选择，最终得到一个近似全局最优的解。

图2 遗传算法流程

（4）遗传算法优化

通过贪心算法得到的一个优质初始解将会作为遗传算法的初始输入。这种组合策略充分发挥了贪心算法的局部搜索优势和遗传算法的全局搜索特点。贪心算法通过在每一步选择当前最优解，快速收敛到一个局部最优解，为遗传算法提供了一个高质量的起点。遗传算法则在此基础上，通过模拟自然选择和遗传机制，对解空间进行全局搜索，进一步优化解的质量。这种组合策略不仅提高了算法的搜索效率，还增强了算法的全局搜索能力，使得最终得到的解更加接近全局最优解。

如图2所示，经过约束分区，目前的约束只剩下软约束，即功耗和距离。功耗约束类似于一维装箱问题，加上距离约束后，这个问题可以看成是一个有冲突的一维装箱问题。在传统的一维装箱问题中，遗传算法的性能最好。遗传算法通常分为基因编码和种群迭代两大部分。在基因编码阶段，我们使用实数编码。与离散编码相比，实数编码提供了更大的解空间，有助于找到更好的解。在群体迭代阶段，我们采用了多样化的交叉和突变技术，以增加跳出局部最优解的可能性。此外，为了提高时间性能，我们采用了空间换时间策略，并引入自适应突变来优化群体质量。

实验结果及分析:

表1 各个算法的分组数量和运行时间

 

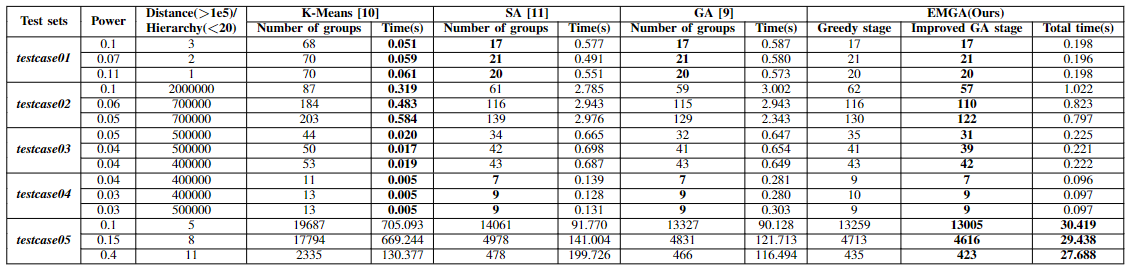
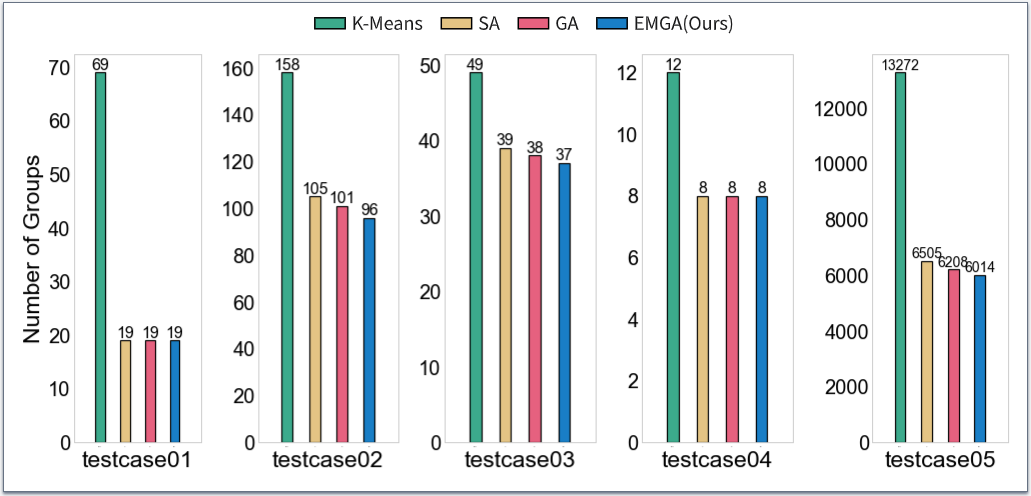
图 3 各个算法分组数量比较

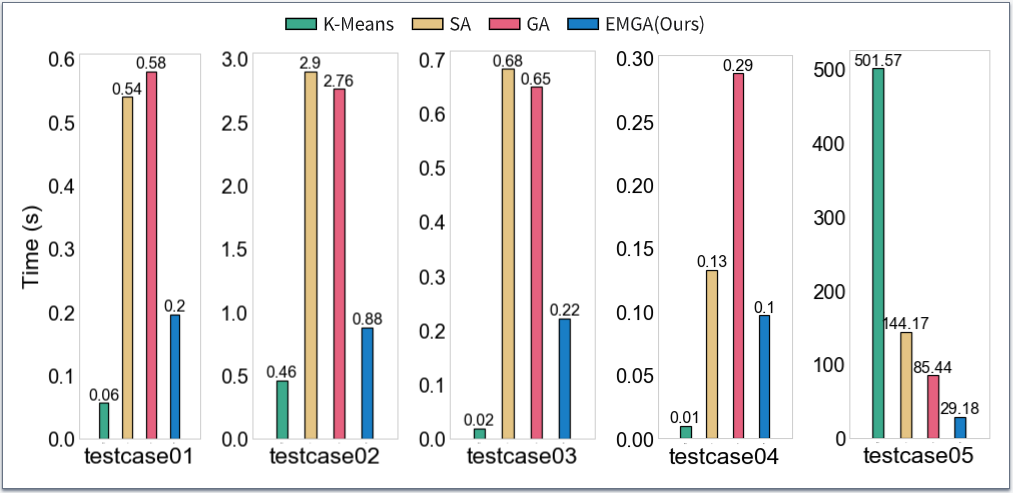
图4各个算法运行时间比较 

如上图实验结果所示，与其他方法比较，EMGA在最为关注的分组质量方面表现最好。EMGA结合了贪心算法和遗传算法的优势。它能快速得到一个初始解，并且能够通过改进的遗传算法维护一个多解集合，其中包含了搜索到的多个优秀解。这些解之间可能存在一定的差异，提供了更多的选择余地。这使得我们的算法比朴素的遗传算法具有更好的性能。相比之下，模拟退火算法和K-Means算法更容易受局部搜索的限制，可能陷入局部最优解。模拟退火算法相对较容易陷入某个解附近，导致生成更多且相似的分组。K-Means算法本身倾向于找到局部最优解而不是全局最优解。

结论:

本文提出一种结合贪心算法和遗传算法的策略，以降低功耗、优化内存块分组并提高内存系统的整体性能。通过利用贪心算法快速找到局部最优解，并将其作为遗传算法的初始解，我们成功地提高了算法的收敛速度和最终解的质量。这种组合策略充分发挥了贪心算法的局部搜索优势和遗传算法的全局搜索特点。实验结果表明，在不同的数据集和约束条件下，所提出的算法在功耗、距离和执行时间上都有显著的性能提升。在初始分组阶段，贪心算法能快速识别相对最优解，并将其与遗传算法相结合，进一步提高算法性能。 

通讯作者简介:

金洲，副教授，中国石油大学（北京）计算机系副教授，入选北京市科协青年人才托举工程、校青年拔尖人才。主要从事集成电路设计自动化（EDA）方面的研究工作。主持并参与国家自然科学基金青年项目、培育项目、重点项目，科技部重点研发微纳电子专项、高性能计算专项青年科学家项目，国家重点实验室开放课题、企业横向课题等。在DAC、TCAD、TODAES、SC、PPoPP、IPDPS、TCAS-II、ASP-DAC等重要国际会议和期刊上发表60余篇高水平学术论文。获EDA2青年科技奖、SC23最佳论文奖、ISEDA23荣誉论文奖、IEEJ九州支部长奖等。

联系方式：jinzhou@cup.edu.cn