中文题目：Mille-feuille：GPU上的分块混合精度单内核共轭梯度解法器

论文题目：Mille-feuille: A Tile-Grained Mixed Precision Single-Kernel Conjugate Gradient Solver on GPUs

录用期刊/会议：37th International Conference for High Performance Computing, Networking, Storage, and Analysis (CCF A)

录用/见刊时间：2024-6-15（录用时间）

作者列表：

1）杨德闯 中国石油大学（北京）人工智能学院 计算机技术 硕21

2）赵雨轩 中国石油大学（北京）人工智能学院 计算机科学与技术 硕22

3）牛一多 中国石油大学（北京）人工智能学院 计算机科学与技术 本21

4）贾伟乐 中国科学院计算技术研究所 研究员

5）邵   恩 中国科学院计算技术研究所 高级工程师

6）刘伟峰 中国石油大学（北京）人工智能学院 计算机系教师

6）谭光明 中国科学院计算技术研究所 研究员

7）金   洲 中国石油大学（北京）人工智能学院 计算机系教师

摘要:

共轭梯度法（CG）和双共轭梯度稳定法（BiCGSTAB）是用于求解稀疏线性系统的有效方法。本文提出了一种新的求解器——Mille-feuille，用于加速GPU上的CG和BiCGSTAB。基于NVIDIA A100和AMD MI210的实验结果表明，Mille-feuille求解器在CG中相比基准实现（包括厂商支持的cuSPARSE/hipSPARSE以及两个最先进的库PETSc和Ginkgo）取得平均3.03倍/2.68倍，5.37倍，4.36倍（最高可达8.77倍/7.14倍，16.54倍，15.69倍）的加速比；在BiCGSTAB中，平均加速比为2.65倍/2.32倍，3.57倍，3.78倍（最高可达7.51倍/6.63倍，16.64倍，11.73倍）；在预条件CG（PCG）中，平均加速比为3.82倍/3.47倍（最高可达40.38倍/47.75倍）；在预条件BiCGSTAB（PBiCGSTAB）中，平均加速比为1.79倍/1.63倍（最高可达45.63倍/44.34倍）。

背景与动机:

在迭代法解法器中，共轭梯度方法和稳定双共轭梯度方法分别因在处理对称正定、非对称或不正定线性系统中的有效性而突出。目前的迭代法解法器往往忽略了一些对性能至关重要的因素，如稀疏矩阵中非零元素数值精度的分布、内核间的同步开销以及解向量x的部分收敛等。本文拟利用稀疏矩阵的数值特征、硬件平台特性以及算法本身的实现原理对共轭梯度解法器进行优化。

设计与实现:

一、稀疏存储格式

我们设计了一种细粒度的两级分块稀疏矩阵存储格式，高级存储以COO的结构捕获块间的信息用于确保SpMV计算过程的负载均衡，并且根据稀疏矩阵中非零元素初始值的范围使用四种不同精度进行存储，对于低级存储，我们使用 CSR 方式来记录块内信息，使用额外的数组记录块内非空行的信息，用于避免在 SpMV 操作期间遍历块中的空行，从而进一步提高 SpMV的性能。

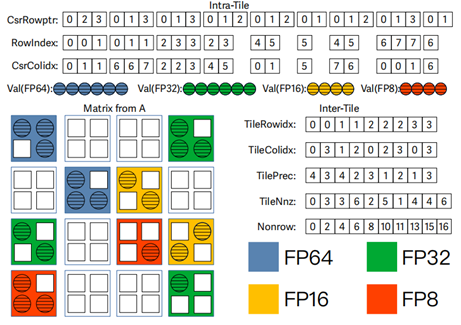
图1. 两级分块的存储结构

二、单内核共轭梯度解法器

接下来，为了减少GPU上不同内核之间的同步开销，我们利用原子操作使整个迭代法求解过程在单个GPU内核内运行。为了实现同步，我们构建多个依赖数组来定义数据和操作之间的依赖关系，并允许原子操作调度warp以执行不同操作的任务。我们根据依赖关系将CG算法分为四个部分，内核启动之前，矩阵A的非空块以负载均衡的方式分配给每个warp并且被加载到共享内存中一次，并在迭代过程中被重复利用，这样可以提升程序的访存效率。

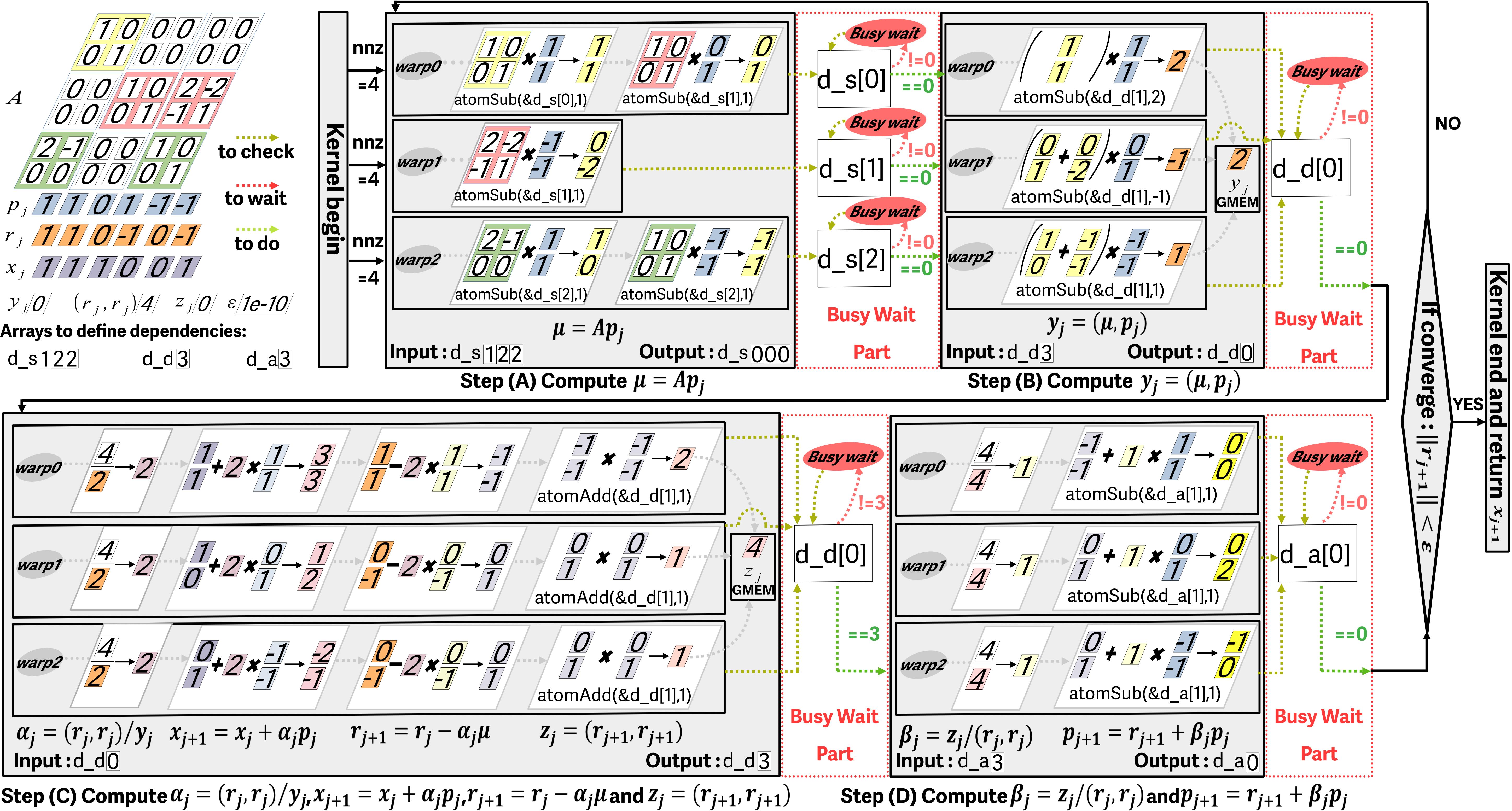
图2. 单内核共轭梯度解法器

三、部分收敛感知混合精度策略

最后，为了在迭代过程中利用解向量x 中已经收敛的元素来优化SpMV的性能，我们根据收敛阈值ε设定了四个范围并实现了一种部分收敛感知混合精度策略，运行时在单个内核内实现块粒度的片上动态精度转换。我们的精度转换仅在共享内存中进行一次，减少了访问全局内存或执行精度转换的高昂开销。

图3. 部分收敛感知混合精度策略

实验结果及分析:

一、Mille-feuille与基准实现的对比（cuSPARSE/hipSPARSE）

在 CG 算法上，与基准实现相比，我们的算法的平均加速比为 3.03 倍和 2.68 倍（最高分别为 8.77 倍和 7.14 倍）。在 BiCGSTAB 算法上，与基准实现相比，我们的算法的平均加速比为 2.65 倍和 2.32 倍（最高分别为 7.51 倍和 6.63倍）。

在PCG算法上，与基准实现相比，我们的算法的平均加速比为 3.82 倍和 3.47 倍（最高分别为 40.38 倍和 47.75 倍）。在PBiCGSTAB 算法上，与基准实现相比，我们的算法的平均加速比为 1.79 倍和 1.63 倍（最高分别为45.63倍和44.34倍）。

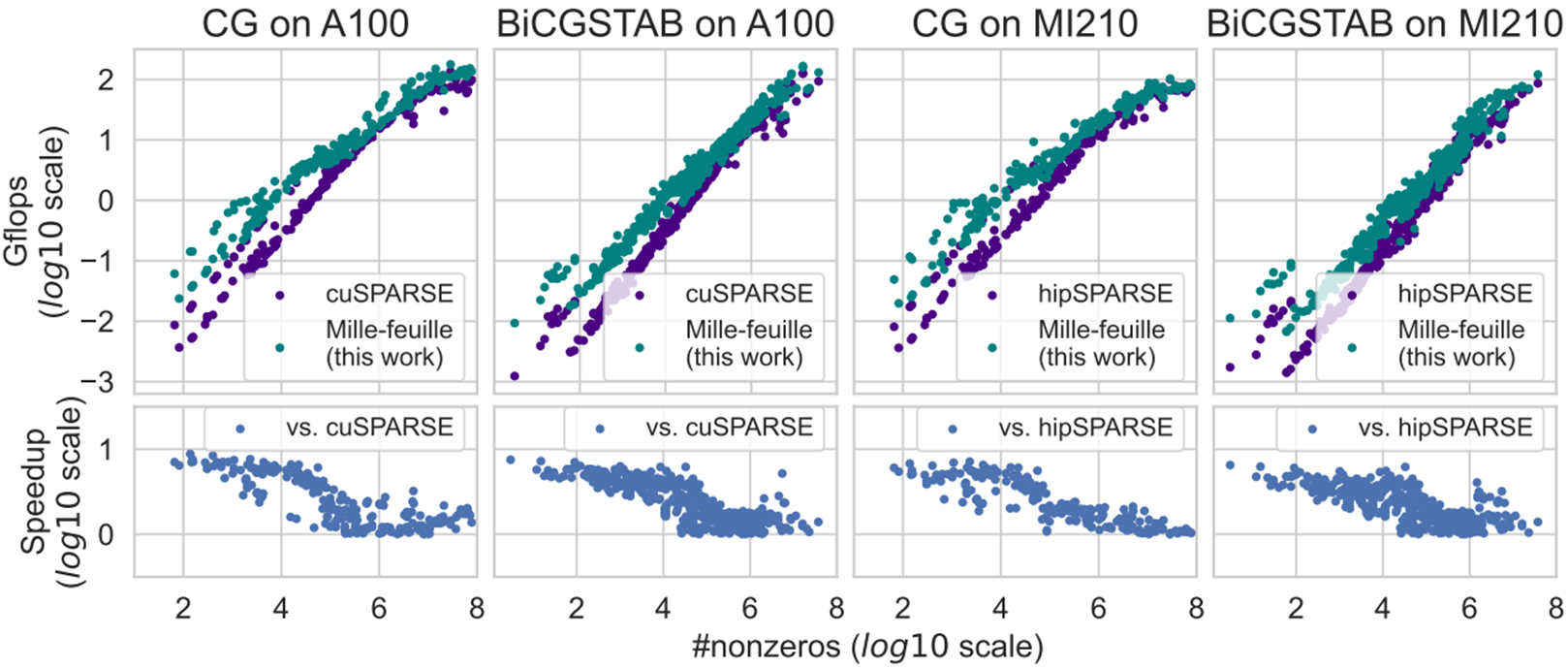
图4. 与cuSPARSE和hipSPARSE实现的CG和BiCGSTAB基准算法的性能比较

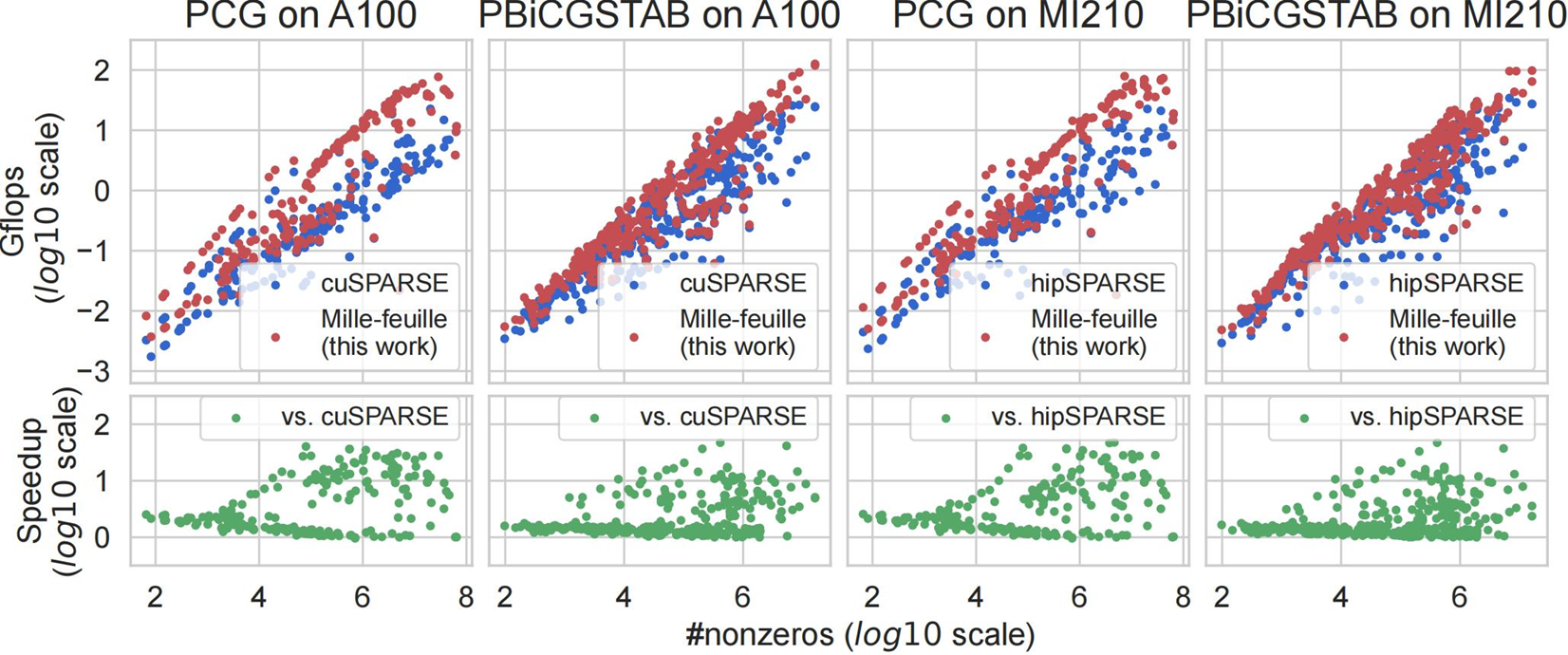
图5. 与cuSPARSE和hipSPARSE实现的PCG和PBiCGSTAB基准算法的性能比较

二、Mille-feuille与PETSc和Ginkgo对比

对于 CG 方法，我们的算法相较于 PETSc 和 Ginkgo分别实现了 5.37 倍和 4.36 倍的几何平均速度提升（最高分别可达 16.54 倍和 15.69 倍）。对于 BiCGSTAB 方法，我们的算法相较于 PETSc 和 Ginkgo 分别实现了3.57倍和 3.78 倍的几何平均速度提升（最高分别可达 16.64 倍和 11.73 倍）。

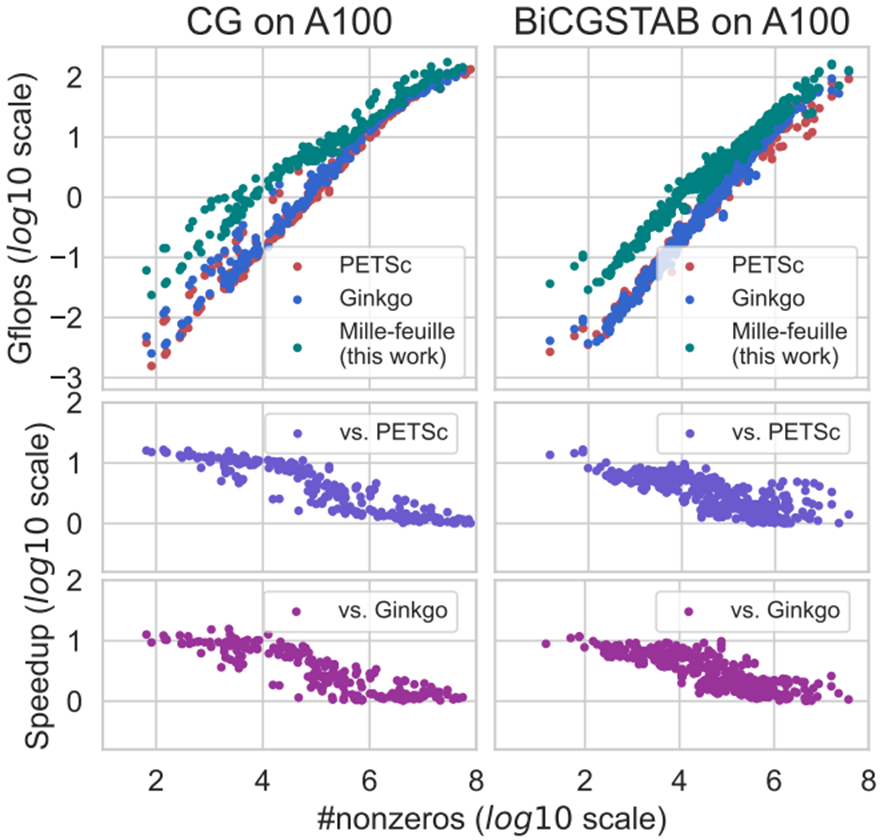
图 6：与PETSc和Ginkgo的性能比较

通讯作者简介:

金洲，副教授.中国石油大学（北京）计算机系副教授，入选北京市科协青年人才托举工程、校青年拔尖人才。主要从事集成电路设计自动化（EDA）、面向科学计算的DSA软硬件协同设计等方面的研究工作。主持并参与国家自然科学基金青年项目、重点项目，科技部重点研发微纳电子专项、高性能计算专项青年科学家项目，国家重点实验室开放课题、企业横向课题等。在DAC、TCAD、TODAES、SC、PPoPP、IPDPS、TCAS-II、ASP-DAC等重要国际会议和期刊上发表60余篇高水平学术论文。获EDA2青年科技奖、SC23最佳论文奖、ISEDA23荣誉论文奖、IEEJ九州支部长奖等。

联系方式：jinzhou@cup.edu.cn