中文题目：在线鞍点问题的近点法

论文题目：Proximal Point Method for Online Saddle Point Problem

录用期刊/会议：The 31st International Conference on Neural Information Processing (ICONIP 2024)（CCF-C类期刊）

录用时间：2024.7.28

作者列表：

1) 孟庆鑫 中国石油大学（北京）人工智能学院 控制科学与工程 博18级

2) 刘建伟 中国石油大学（北京）人工智能学院 自动化系 教师

摘要:

本文主要研究在线鞍点问题，涉及一系列两人时变凸凹博弈。考虑到环境的非平稳性，我们采用对偶间隙动态纳什均衡后悔函数作为算法的性能指标设计。我们提出了近端点法的三种变体：在线近点法（OPPM）、乐观OPPM（OptOPPM）和具有多个预测因子的OptOPPM。每种算法都保证了对偶间隙和动态纳什均衡后悔函数的上限，当与对偶间隙后悔函数进行比较时，实现了接近最优后悔上界。具体来说，在某些良性环境中，例如平稳回报函数序列，这些算法保持了一个几乎恒定的后悔上界。实验结果进一步验证了这些算法的有效性。最后，本文讨论了使用动态纳什均衡后悔上界作为性能指标的潜在可靠性问题。技术附录和代码可以在以下网址获取https://github.com/qingxin6174/PPM-for-OSP.

背景与动机:

在线鞍点（The Online Saddle Point）问题涉及一系列两人时变凸凹博弈。在第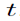轮中，玩家1和2共同选择一对策略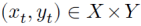。在这里，玩家1将收益最小化，而玩家2将收益最大化。两位玩家没有对当前或未来收益函数的先验知识。在最终确定策略对后，环境显示了一个连续的收益函数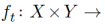ℝ，它满足以下条件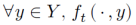：在𝑋上是凸的，并且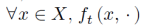在𝑌上是凹的。没有对环境施加额外的假设，从而允许潜在的规律性甚至对抗性行为。目标是为玩家提供近似纳什均衡的决策算法，确保玩家在大多数回合中的决策接近鞍点。

主要内容:

我们提出了解决OSP（The Online Saddle Point）问题的近点法的三种变体：在线近点法（the Online Proximal Point Method，OPPM），乐观OPPM（the Optimistic OPPM，OptOPPM）允许任意预测器，OptOPPM具有多个预测器，增强了算法处理多个预测器的能力。结果如表1所示。

表1：论文的结果总结。

在该表中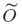，包含了多项式对数因子，表示凸凹收益函数序列的累积差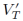，表示单个预测器的累积误差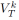，表示第𝑘个预测器的累积误差。

结论:

本研究通过引入三种自适应性算法来解决在线鞍点问题近端点法：OPPM、OptOPPM和OptOPPM多个预测器。这些方法是为了维持D-Gap (The duality gap) 以及NE-Reg (The dynamic Nash equilibrium regret)的上界而精心设计的，确保与D-Gap相关的性能接近最优。在有利条件下，如取不变的收益函数，三种自适应性算法OPPM、OptOPPM和OptOPPM保持接近不变的后悔度量上限。该研究还质疑了NE-Reg作为后悔度量函数的有效性，并通过实验支持了我们的质疑和观点。

作者简介:

刘建伟，教师，学者。发表学术研究论文280多篇。