序列测量下量子内在随机性的量化
中文题目：序列测量下量子内在随机性的量化
论文题目：Quantifying the intrinsic randomness in sequential measurements
录用期刊/会议：New Journal of Physics （中科院大类二区，JCR Q2）
原文DOI：10.1088/1367-2630/ad19fe
原文链接： https://iopscience.iop.org/article/10.1088/1367-2630/ad19fe
作者列表：
1） 刘新建 中国石油大学（北京）人工智能学院 计算机科学与技术 硕21
2）王玉坤 中国石油大学（北京）人工智能学院 计算机科学与技术系 教师
3）韩云光 南京航空航天大学 计算机科学与技术学院 副研究员
4）武 霞 中央财经大学信息学院 副教授
文章简介:
序列测量场景中的量子测量通常涉及半正定算子测量，由POVM定义的一般测量比投影测量在设备无关随机性认证时更具有优势。与投影测量不同，在用于POVM的量子设备中存在额外和隐藏自由度，量化其中的随机性是具有挑战的。此外，在实际设备中由于环境和噪声的影响会引入经典的随机性，刻画其中的随机性也需要考虑如何去除经典随机性的影响。给定一组POVM可能有无限多种方法来构造检测设备，这种隐藏的信息会泄漏给不可信第三方Eve，所以在刻画POVM量子设备的随机性时需要考虑这种隐藏信息的影响。在序列测量下刻画随机性时，除了考虑上述因素，还需要考虑序列方轮与轮之间的关联造成的影响。虽然在理论上可以在序列测量下从一对纠缠的量子源获得无界的随机比特位，但是从一对纠缠的量子源中可以鲁棒地产生多少随机性还有待研究。本文对序列测量方案中产生的量子内在随机性进行了严格定义，并在设备不同可信程度下量化了序列测量方案中三维最大纠缠态和最大违背态产生的量子内在随机性。
摘要:
在标准贝尔场景中，当对量子系统进行局部投影测量时产生随机性的数量是有限的，通过对其系统进行序列测量可以被打破这一限制。然而，除了在设备无关场景中使用半正定规划方法量化随机性外，在序列测量方案中还未建立严格的随机数定义。本文定义了序列测量中的量子随机性，并量化了CGLMP不等式序列场景下的随机性。首先，我们研究了序列投影测量下混合态的量子内在随机性，以及纯态下序列POVM下的内在随机性。结合以上推导，自然地，我们严格定义了任意量子态下序列POVM的量子内在随机性。此外，我们将我们的方法应用于一个Alice和两个Bob序列测量场景，在设备可信方案下通过给出的极值分解形式量化了最大纠缠态和最大违背态的量子内在随机性。在设备无关方案下，量子态和测量都可能包含噪声，使用序列NPA层次结构方法得到了可验证随机数的下界。
设计与实现:
本文主要考虑了单边序列测量下随机性的定义，该模型已被广泛提出并用于研究序列测量之间的非局域共享。我们根据监听者Eve和量子设备之间不同关联程度，推导得到了监听者Eve的经典最大猜测概率和量子最大猜测概率，然后使用条件最小熵刻画其中的随机性。首先在序列测量方案下建立了量子内在随机性的定义，包括不可信量子态、不可信序列POVM以及不可信量子态和测量场景。然后，利用本文对序列测量随机性的定义以及序列NPA半正定规划方法，量化了三维最大纠缠态和最大违背态在设备可信和不可信场景中产生的内在随机性。此外本文对随机性的定义不限于每一个Bob是独立的，还可以扩展到允许经典信号传输的场景。
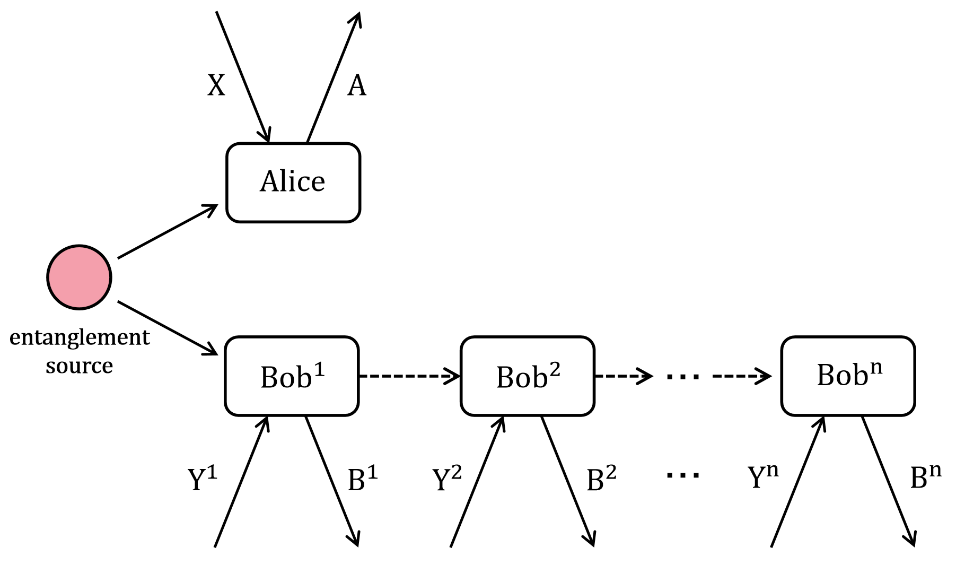
单边序列测量场景
1.不可信量子态随机性的定义
Eve可能通过随机变量与量子系统产生经典相关性。具体来说，Eve可以抽样大量随机变量
的值，并使用这些信息来预测量子系统的测量结果。
经典最大猜测概率
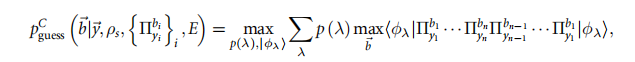
监听者还可以通过纯化与量子系统产生量子相关性，Eve在已知量子侧信息的情况下预测量子系统的测量结果。
量子最大猜测概率
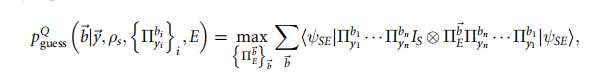
2.不可信序列POVM随机性定义
经典最大猜测概率
POVM集合和量子态集合一样，也是一个凸集。所以Eve也可以通过随机变量与量子系统产生经典相关性。
量子最大猜测概率
本文通过Naimark扩展，主系统的一般POVM测量可以被视为由主系统和辅助系统
组成的复合系统的投影测量，定义了监听者Eve的量子最大猜测概率。
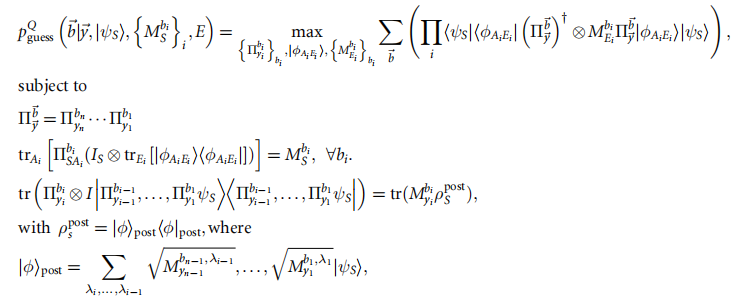
3.不可信量子态和测量随机性定义
结合以上推导，考虑最一般的场景即量子态和测量都不可信
经典最大猜测概率
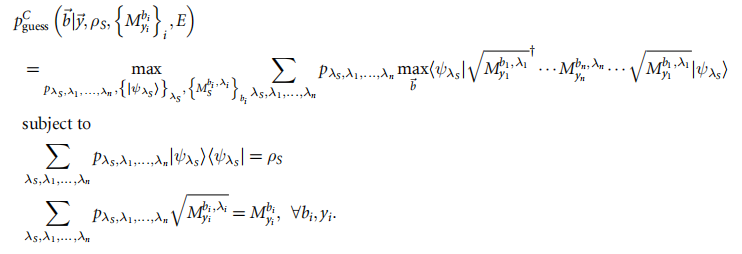
量子最大猜测概率
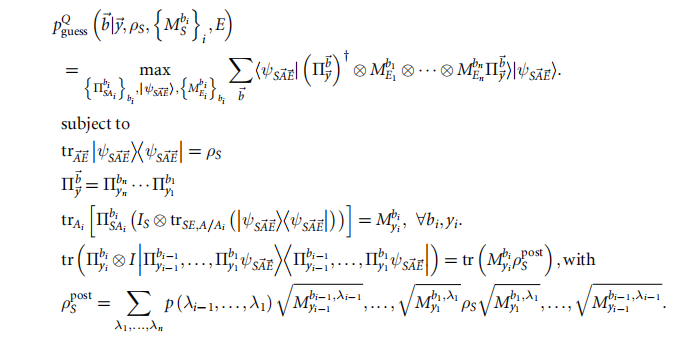
实验结果及分析:
1.设备可信方案下内在随机性的量化
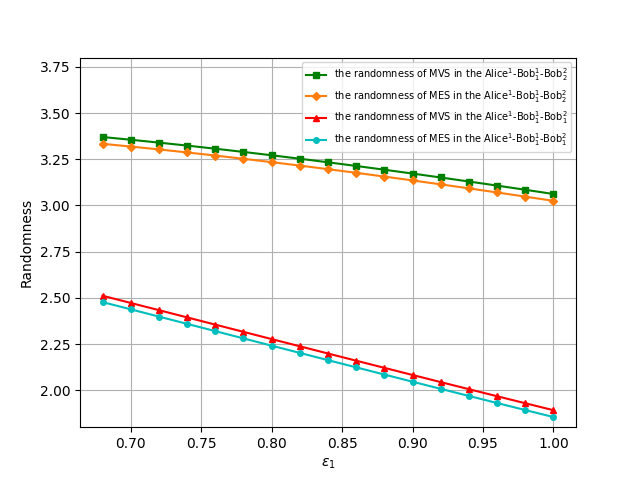
图中展示了最大违背态与最大纠缠态之间全局内在随机性的比较。从图中可以看出，随着Bob方弱测量系数的增大，越接近投影测量时产生的随机性越小。结果表明，在序列CGLMP测量场景中，与最大纠缠态相比，最大违背态展示出了更大的随机性。
2.设备无关方案下内在随机性的量化
在设备可信方案中，我们利用上述随机性的定义以及给出的特殊POVM分解形式量化了最大纠缠态和最大违背态的随机性，在设备无关方案中，使用半正定规划方法序列NPA层级约束量化了其中的随机性。
此外我们还分别比较了不同测量基下的随机性。从下图中可以看出在设备可信方案下
和
选择不同的测量基展现的随机性更大。在设备无关方案中，也会出现类似的结果。
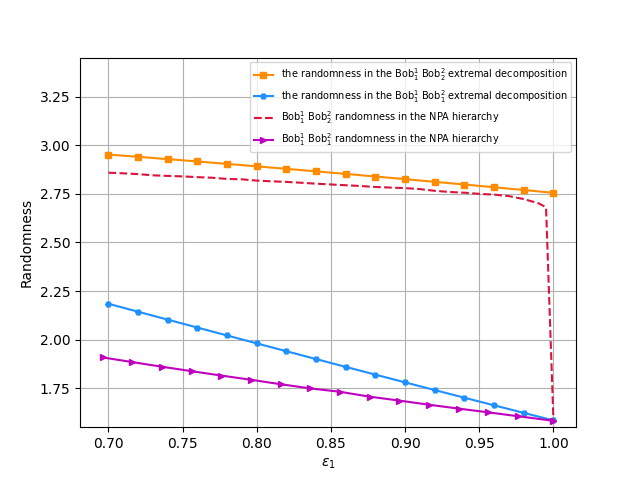
最大纠缠态在设备不同可信程度下产生的随机性
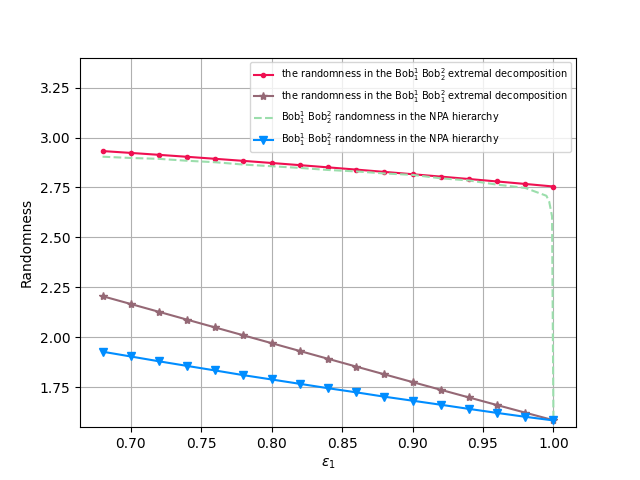
最大违背态在设备不同可信程度下产生的随机性
结论:
本文严格定义了序列测量下量子系统产生的内在随机性。为了实现这一目标，本文基于窃听者Eve与量子系统之间的不同关联程度，推导了Eve的经典最大猜测概率和量子最大猜测概率。此外，在设备的不同可信程度下，量化了CGLMP序列测量场景下的量子内在随机性。在可信量子系统场景中，量子态是纯态、最大纠缠态或最大违背态，并且只有测量含有噪声，在这种情况下，Eve的量子最大猜测概率和经典最大猜测概率相同，因此只需考虑POVM极值分解来最大化猜测概率。对于CGLMP场景下的POVM，本文提供了一种特殊的分解形式，并计算了这种分解结果的随机性。这种特殊的分解提供了随机性的上限估计。原则上，应该遍历POVM的所有极值分解来量化随机性。然而，提供所有分解形式尤其是对于高维POVM来说是具有挑战性的。在未来的研究中，将进一步探索高维POVM极值分解方法，以获得更准确的结果。在设备无关方案中，量子态和测量都是不可信的，我们使用顺序NPA层次结构方法来量化高维系统中最大纠缠态和最大违背态可验证的随机性的下界。
作者简介:
王玉坤，女，博士，人工智能学院计算机系助理教授。研究方向为量子计算，量子密码及量子信息基本理论，主要包括：量子机器学习，经典困难问题量子算法加速，量子线路优化与映射，量子密码协议设计及安全性证明，设备不可信量子信息处理等。主持国家自然基金青年基金，密码管理局密码科技国家重点实验室面上项目，校人才启动基金，在国内外著名期刊和会议发表SCI检索的学术论文30余篇。担任多个国际顶级期刊审稿人。