论文题目：三维地震数据频域无监督随机噪声压制方法

录用期刊/会议：石油地球物理勘探 (EI中文期刊)

原文DOI：10.13810/j.cnki.issn.1000-7210.2023.06.003

作者列表：

1） 薛亚茹 中国石油大学（北京） 信息科学与工程学院/人工智能学院 电子系教师

2） 苏军利 中国石油大学（北京） 信息科学与工程学院/人工智能学院 研21

3） 冯璐瑜 中国石油大学（北京） 信息科学与工程学院/人工智能学院 博20

4） 张   程 中国石油大学（北京） 信息科学与工程学院/人工智能学院 研21

5） 梁   琪 中国石油大学（北京） 信息科学与工程学院/人工智能学院 研21

摘要:

提高数据信噪比是地震资料处理中的关键环节。目前基于深度学习的降噪方法已取得较好效果。但该类方法以数据局部相似性为前提，采用时空域数据分窗进行处理，运算效率往往较低。考虑到地质结构的连续性，炮间数据具有一定的相似性，利用其同频率分量的低秩特点，设计了一种三维数据频域降秩的深度学习去噪方法。首先阐明三维数据的频域低秩原理，采用奇异值分解理论指导建立自编码神经网络；考虑频域随机噪声的分布特点，采用K-L(Kullback-Leibler)散度约束损失函数，改善了去噪效果。通过对合成记录和实际资料处理，并与多通道奇异谱分析(Multichannel Singular Spectrum Analysis，MSSA)及K-SVD(K-奇异值分解)方法对比，验证了该方法在去噪效果和计算效率等方面的优势。

算法设计:

地震勘探通过多炮激发实现地下构造反射成像。为提高成像精度，震源在探区多次激发，构成了炮点坐标、检波点坐标及时间的五维地震数据，可表示为。为方便解释，以一条测线的炮集为例进行分析，但同样适用其他三维数据体。假设地层是水平层状介质，第炮数据可表示为，则第炮记录可表示为

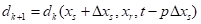
(1)

式中：△x_s为炮间距；为射线参数。变换到频率域，有：

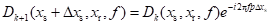
(2)

由上式可知，相邻炮记录之间的频谱仅有线性相位差。对某个频率而言，各炮数据构成低秩矩阵，可以表示为：

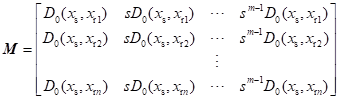
(3)

其中，的奇异值分解可表示为

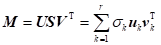
(4)

根据上述分析，频率切片会呈现一定的低秩特征(或稀疏性)，对任一炮的某一频率分量可以表示为特征向量的稀疏表示，即

(5)

式中：表示第炮频率分量；为稀疏表征参数。通过适当的降秩，可以达到压制噪声的目的。

对于自编码网络，输入数据为X，编码器函数可表示为：

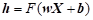
(6)

该过程期望获得数据的稀疏编码。与式(5)相比，实质就是寻找稀疏编码系数；编码器各神经元的权重系数近似为式(5)中的特征向量矩阵的转置，但没有各特征向量的正交性限制。自编码网络可以通过神经网络的训练过程优化各特征向量，打破正交约束，大大提高数据特征的稀疏性。

解码器函数可以表示为：

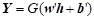
(7)

该过程即为式(6)的逆过程，利用编码器的稀疏系数重构数据。在整个过程中由于压缩作用，会将不相干的噪声压制，而只保留相干性较强的有效信号。

通过上述分析可见，自编码网络工作原理与奇异值分解相似，这为自编码网络提供了工作机理，克服了神经网络的黑箱特性。图1解释了自编码网络与奇异值分解在结构和原理上的对应关系。

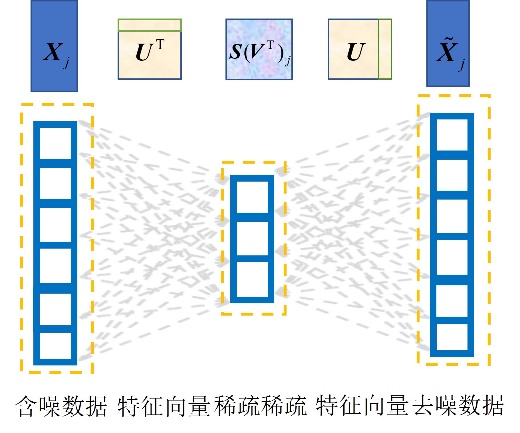
图1 自编码网络与奇异值分解原理映射图

基于上述自编码网络去噪原理，设计了无监督网络模型，如图2所示，利用SVD分解后特征值能量占比为90%时对应的阶数，作为中间层维度的参考。此策略保证自编码网络的稀疏度低于SVD方法，能学习到更稀疏的数据特征。

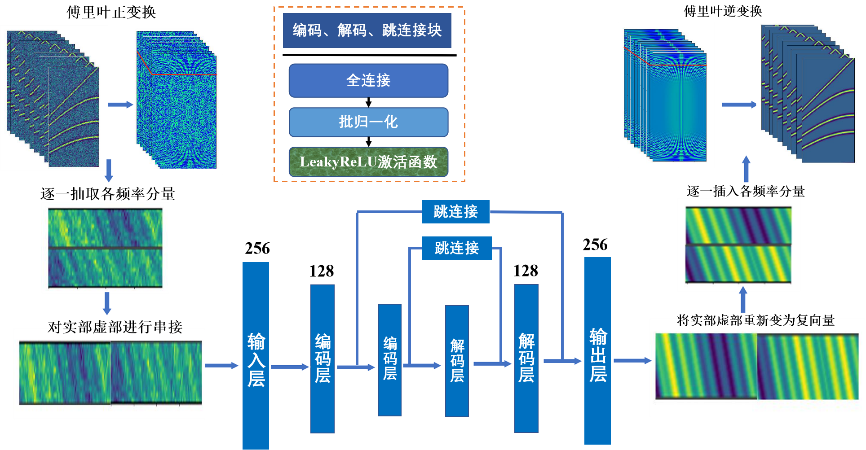
图2 无监督去噪模型框架

根据Bayes反演理论，最小化均方误差函数是以零均值高斯白噪声为假设条件。但是由于本文方法是在频率域完成，白噪声的存在导致频率切片的均值偏移，因此对去噪结果进行均值约束，有利于数据归位于其真值。本文采用KL散度进行约束，损失函数优化为：

(8)

式中：，表示对去噪后数据取均值；为参考均值，理论上应该等于干净信号的均值。

实验分析:

图3a是原始含噪道集，噪声导致同相轴的清晰度降低；图3b为K-SVD方法去噪结果及残差道集，可以看出，噪声去除并不彻底，尤其是远炮检距仍然可以看到大量噪声存在；图3c为MSSA方法去噪结果及残差剖面，噪声得到了有效压制，但是同相轴的连续性并未得到恢复，并且残差道集中有明显的有效信号痕迹；图3d是本文方法去噪结果及残差剖面，噪声压制比较彻底、同相轴更清晰，残差道集中有效信号不明显。图4展示了K-SVD、MSSA和本文方法去噪结果与去除的噪声之间的相似性，可见：K-SVD方法处理后在2.4~3.2 s大炮检距处，残差信号与去噪结果存在较高的相似性，说明去噪结果中仍然保留了部分噪声，压制不彻底；经过MSSA方法去噪后的数据在1.8~3.4 s除了大炮检距处噪声残留，对有效信号损伤也较大，这在图3c的残差道集上也很明显；而本文方法去除的噪声与保留的信号相干性较小，说明在去噪时没有损伤有效信号，具有较高的保真度。

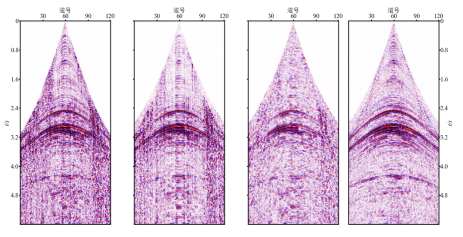
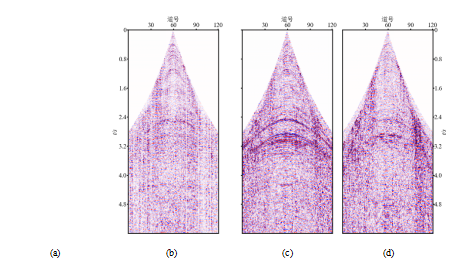
图3 三种方法实际地震数据二去噪对比

(a)原始道集；(b)K-SVD法去噪结果(上)及其残差(下)；(c)MSSA法去噪结果(上)及其残差(下)；(d)本文方法去噪结果(上)及其残差(下)

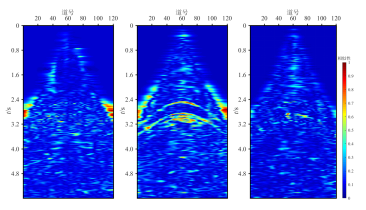
图4 三种方法去噪结果与残差的局部相似性对比

(a)K-SVD法；(b)MSSA法；(c)本文方法

作者简介:

薛亚茹，副教授，博士，中国石油大学（北京）信息科学与工程学院/人工智能学院副教授，博士生导师，UIUC大学访问学者。主要从事地震信号处理、反演、人工智能等方面研究。