中文题目：污水处理厂的无模型自适应非奇异快速积分终端滑模控制方法

论文题目：Model-Free Adaptive Nonsingular Fast Integral Terminal Sliding Mode Control for Wastewater Treatment Plants

录用期刊/会议：Applied Sciences (JCR Q2)

原文DOI：https://doi.org/10.3390/app132413023

原文链接：https://www.mdpi.com/2076-3417/13/24/13023

录用/见刊时间：2023.12.6

作者列表：

1） 徐宝昌 中国石油大学（北京）信息科学与工程学院/人工智能学院 自动化系 教师

2） 王中军 中国石油大学（北京）信息科学与工程学院/人工智能学院 控制科学与工程专业 硕21

3） 刘忠尧 中国石油大学（北京）信息科学与工程学院/人工智能学院 控制科学与工程专业 硕21

4） 陈贻祺 中国石油大学（北京）信息科学与工程学院/人工智能学院 控制科学与工程专业 博21

5） 王雅欣 中国石油大学（北京）信息科学与工程学院/人工智能学院 控制科学与工程专业 博19

文章简介:

本文的主要贡献在于针对污水处理厂难以精确建模以及存在未知干扰等特点，建立了污水处理厂的紧格式动态线性化数据模型，并提出了一种数据驱动的无模型自适应非奇异快速积分终端滑模控制方法。本文方法的优势如下：

(1)本文所提方法不需要污水处理厂的数学模型，仅需要实时I/O测量数据。因此该方法能有效避免模型的不确定性以及未建模动态对闭环系统的影响。

(2)针对传统积分滑模控制不能保证系统状态在有限时间内收敛到零以及跟踪误差收敛速度慢的问题，提出了一种新的快速积分终端滑模面，以保证跟踪误差在远离平衡点时能够快速收敛。

(3)基于国际基准仿真平台BSM1对所提出方法的控制效果进行了验证并与PID和MPC等方法的控制效果进行了比较。研究结果表明，本文提出的MFA-NFITSMC方法在污水处理过程的控制中具有更好的跟踪性能和更强的鲁棒性。

摘要:

污水处理厂（WWTP）由于其复杂的生化特性而难以进行有效控制，并且由于可测变量的局限性，难以建立其精确的数学模型。针对以上问题，本文提出了一种无需数学模型，仅需要输入/输出(I/O)数据的无模型自适应非奇异快速积分终端滑模控制（MFA-NFITSMC）算法来实现对污水处理厂的控制。首先，基于动态线性化的概念，建立污水处理厂的紧格式动态线性化(CFDL)数据模型。然后，提出了一个新的快速积分终端滑模面(FITSMS)以加快跟踪误差的收敛速度，并结合动态线性化数据模型设计了离散时间无模型自适应非奇异快速积分终端滑模控制器，通过理论分析证明了闭环系统的稳定性。最后，基于国际基准仿真平台Benchmark Simulation Model No.1（BSM1）进行对比实验，结果表明，本文方法在污水处理厂的控制上具有更高的跟踪精度和更强的鲁棒性。

背景与动机:

随着经济快速发展及城市工业化进程的推进，工业污水和生活废水的排放日益加剧，水污染引起的可用水短缺和日益增长的用水需求，严重加剧了水的供需矛盾，已成为全世界面临的共同难题。污水处理厂是一种广泛应用于石油化工、居民生活等领域的工业系统，其能够减少水污染，促进废水循环利用，大大降低了工业用水需求，避免了环境污染。然而，污水处理厂是一个非常复杂的时变动态系统，其内部的反应过程受到进水流量、污染物负荷以及未知进水组分的影响，呈现出非线性、强耦合和强扰动等特点。因此，针对污水处理厂的控制研究对于改善运行性能、提高出水水质具有重要意义。

设计与实现:

（1）基准仿真模型BSM1

为有效评价污水处理控制策略，欧盟科学技术合作组织（COST）和国际水质协会（IWAQ）联合开发了活性污泥法的基准仿真模型BSM1[24]。该模型包含生化反应池和二沉池两部分，其总体布局如图1所示。生化反应池由5个单元组成，前2个单元为缺氧池，主要发生反硝化反应将硝态氮还原为氮气；后3个单元为好氧池，主要发生硝化反应将氨氮氧化成硝酸盐。生化反应的机理模型采用IWAQ提出的活性污泥1号模型（activated sludge model No.1，ASM1），该模型包括13种组分，8个生化反应过程及19个参数。经过生化反应池后的污水进入二沉池，二沉池划分为10层，其主要作用是通过沉淀进行泥水分离，沉淀后上层清水排出，下层污泥一部分被送至生化反应池参与反应，一部分排出系统。二沉池的机理模型采用双指数沉淀速度模型。

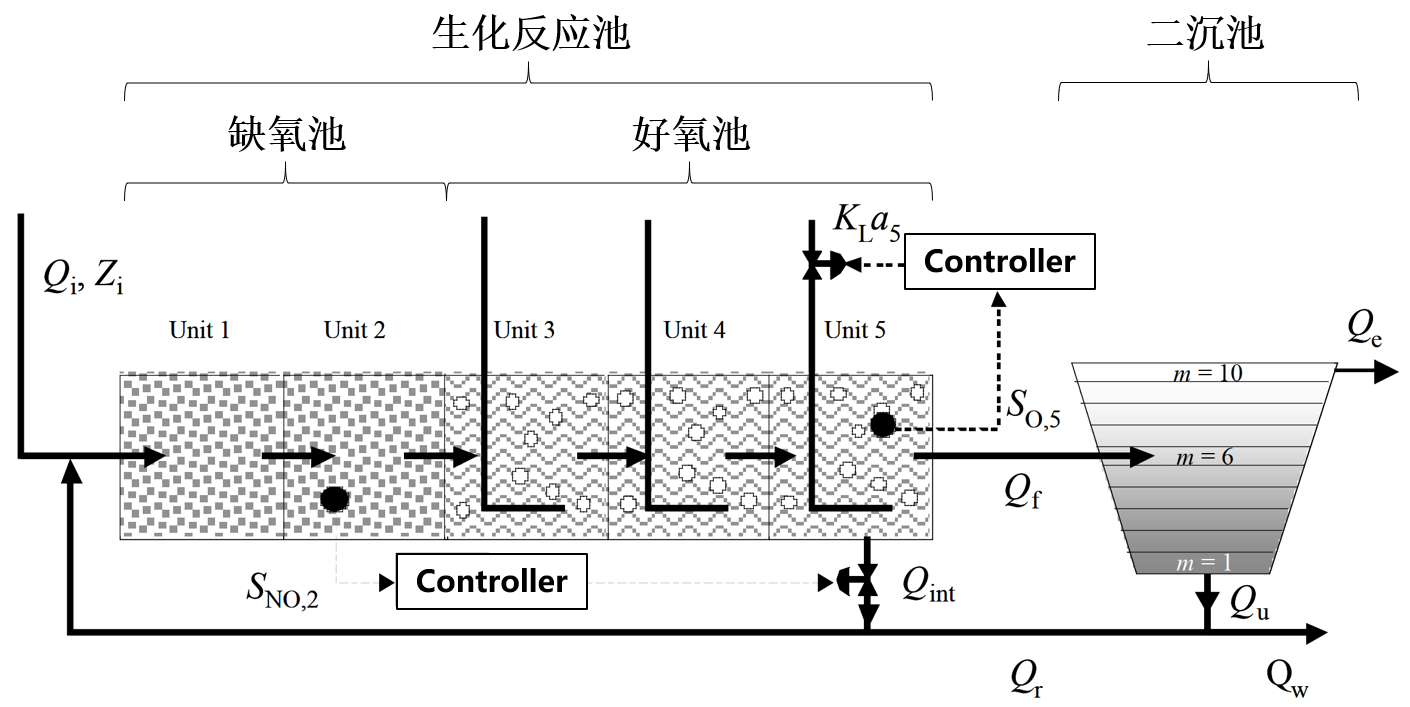
图1 BSM1工艺流程图

（2）污水处理厂的动态线性化模型

以溶解氧浓度为例，污水处理厂 控制过程的离散非线性系统可表示为：

根据引理可得，当时，一定存在一个被称为伪偏导数（pseudo partial derivative，PPD）的时变参数，使系统可转化为如下CFDL数据模型：

针对动态线性化数据模型中的未知伪偏导数，采用改进投影算法进行估计，考虑如下PPD估计准则函数：

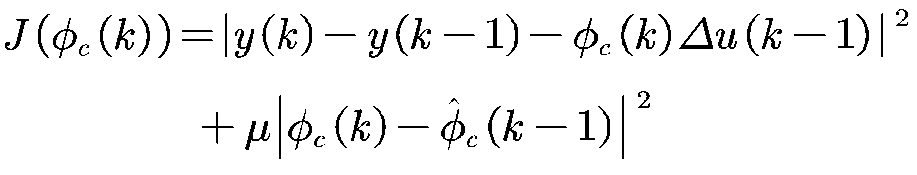
上式关于求极值可得：

（3）快速积分终端滑模面

滑模控制的设计分为两个阶段：（1）设计滑模面，迫使系统状态到达系统的平衡点（2）设计趋近律，保证系统的运动轨迹被驱动到滑模面上并保持。传统的滑模控制在到达阶段无法保证系统的鲁棒性，为解决该问题，引入积分滑模控制(ISMC)来消除到达阶段，同时，为了保证系统状态在有限时间内收敛到零并加快收敛速度，本文提出了如下快速积分终端滑模面：

由于污水处理过程存在进水流量及未知组分浓度的干扰，溶解氧浓度的跟踪误差无法一直处于滑模面上，这将导致系统的全局鲁棒性恶化。为了满足跟踪误差对滑模面的可达性，同时加快收敛速度和减小抖振，选择如下趋近律：

（4）MFA-NFITSMC算法

结合污水处理厂的动态线性化模型和快速积分终端滑模面，可得MFA-NFITSMC控制方法的控制率：

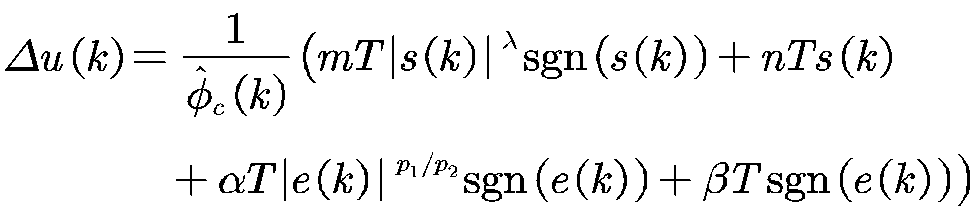
基于MFA-NFITSMC控制方法的污水处理厂控制系统框图如图所示：

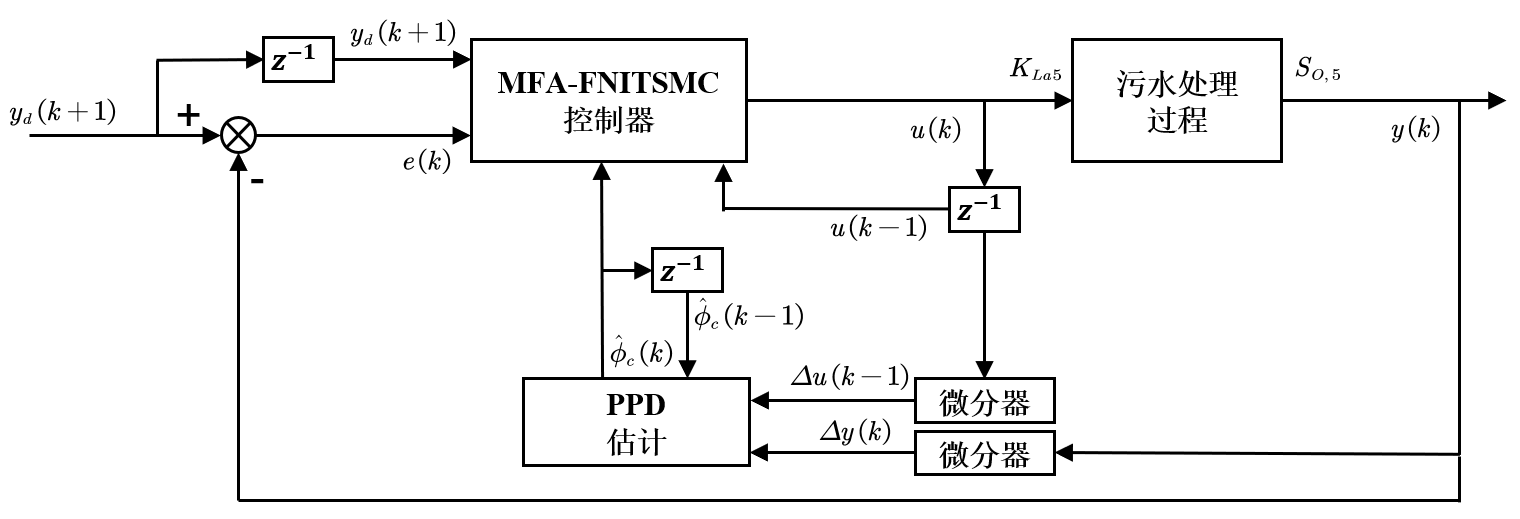
图2 控制系统框图

主要内容:

本文的主要贡献在于针对污水处理厂难以精确建模以及存在未知干扰等特点，建立了污水处理厂的紧格式动态线性化数据模型，并提出了一种数据驱动的无模型自适应非奇异快速积分终端滑模控制方法。本文方法的优势如下：

(1)本文所提方法不需要污水处理厂的数学模型，仅需要实时I/O测量数据。因此该方法能有效避免模型的不确定性以及未建模动态对闭环系统的影响。

(2)针对传统积分滑模控制不能保证系统状态在有限时间内收敛到零以及跟踪误差收敛速度慢的问题，提出了一种新的快速积分终端滑模面，以保证跟踪误差在远离平衡点时能够快速收敛。

(3)基于国际基准仿真平台BSM1对所提出方法的控制效果进行了验证并与PID和MPC等方法的控制效果进行了比较。研究结果表明，本文提出的MFA-NFITSMC方法在污水处理过程的控制中具有更好的跟踪性能和更强的鲁棒性。

实验结果及分析:

为验证所设计方法的控制效果，将MFA-NFITSMC应用于图1所示的BSM1中。图3中展示了晴天和雨天第7-14天的动态进水数据和关键组分浓度，其中包含进水流量，易生物降解底物和氨氮，采样间隔为15分钟，总运行时间为2周，前一周的进水数据用于稳定系统，后一周的动态数据用于测试控制器性能。针对系统控制效果的评价，主要基于以下指标：

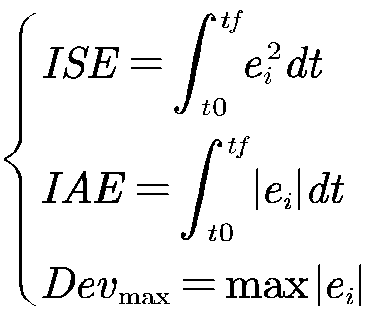
情况1：正常情况下，当第五单元DO浓度保持在时出水水质达标，因此在该情况下将DO参考轨迹设置为，考虑进水流量和组分浓度的外部干扰，分别在晴天和雨天对控制器性能进行测试，并与其他方法进行比较。

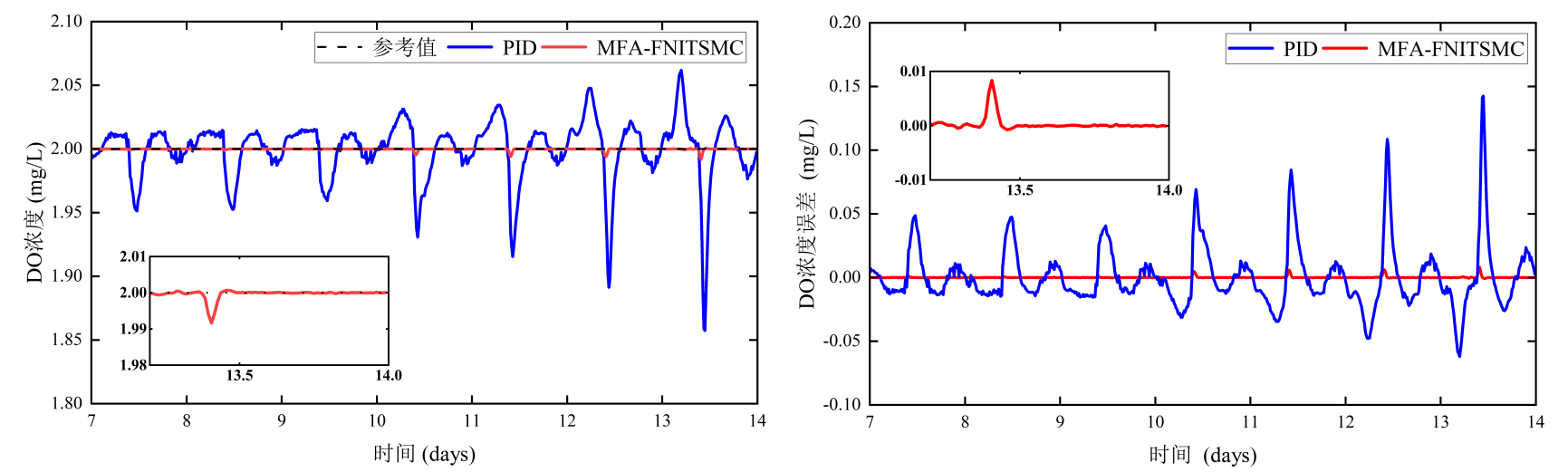
(a) DO浓度 (b) DO跟踪误差

图3 晴天DO控制效果

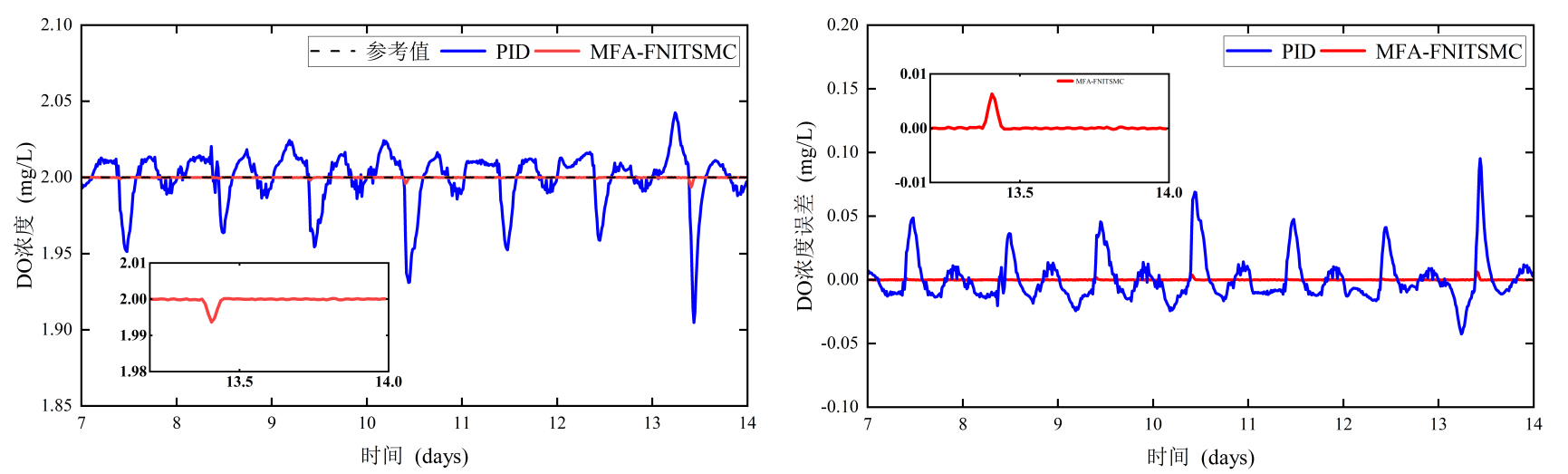
(a) DO浓度 (b) DO跟踪误差

图4 雨天DO控制效果

表1 情况1中晴天工况不同算法控制性能对比

表2 情况1中雨天工况不同算法控制性能对比

情况2：采用某实际污水处理厂的进水数据用于测试MFA-NFITSMC，这表明WWTP受到的外部扰动是随机的而非周期性的。采用三种不同类型的参考轨迹：（1）时不变参考轨迹。（2）时变参考轨迹，第0天到第1天，；第1天到第1.5天，；第1.5天到第2天，；第2天到第2.5天，；第2.5天到第3天，。（3）采用DO浓度实际参考轨迹。

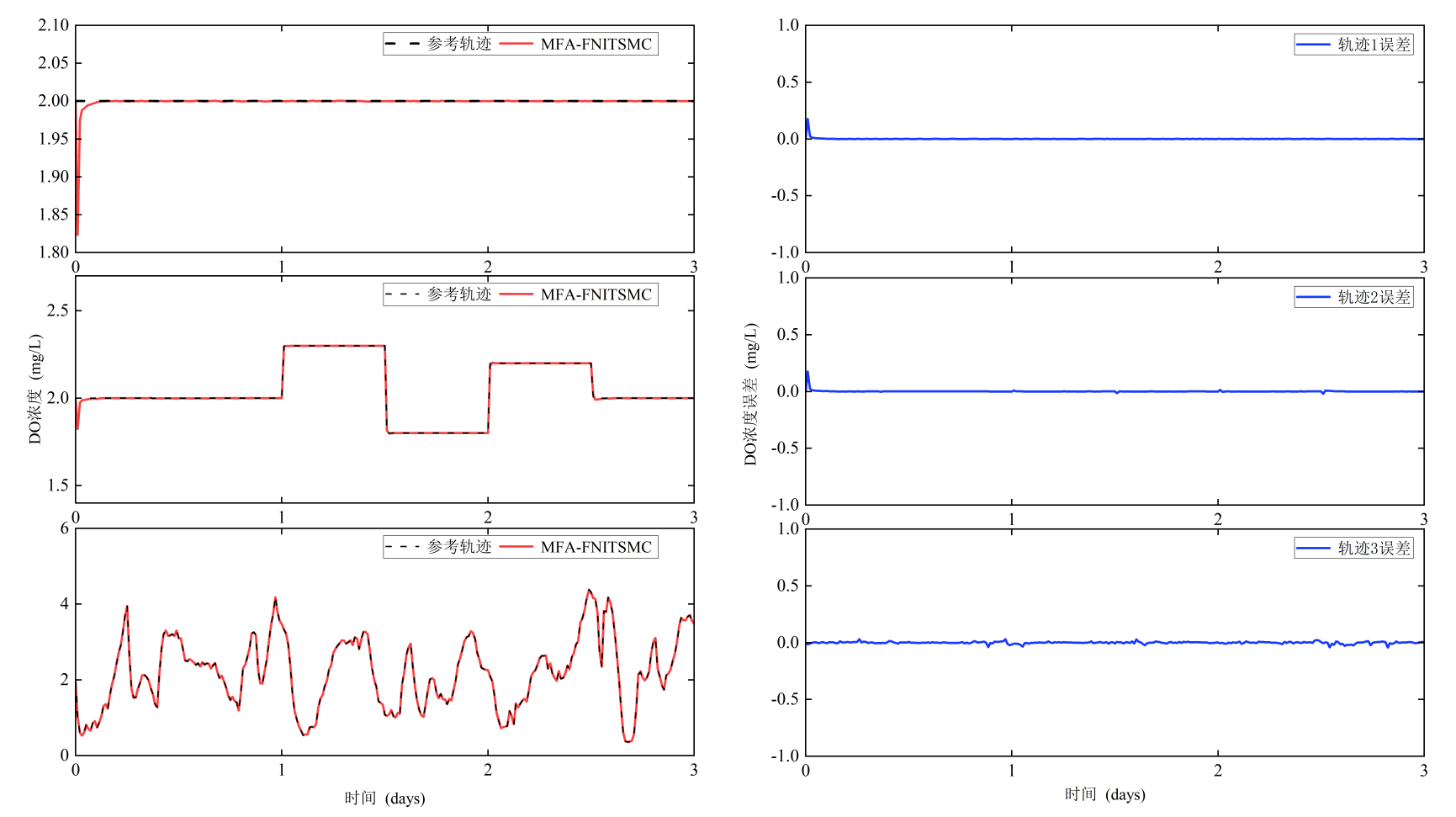
(a) 不同参考轨迹下的DO控制效果 （b）不同参考轨迹下的DO跟踪误差

图5 实际进水数据下的DO跟踪效果

表3 情况2中使用实际数据下的MFA-NFITSMC控制性能指标

情况3：和作为污水处理过程的关键指标需要控制在合理范围内，但通过调节内回流量来控制时，也会对造成较大的干扰，传统方法难以对和同时进行有效控制。为验证本文所提方法的控制效果，在雨天工况下采用两个独立的MFA-NFITSMC控制器分别控制第二单元硝态氮浓度和第五单元解氧浓度，硝态氮浓度参考轨迹设置为，DO参考轨迹设置为。

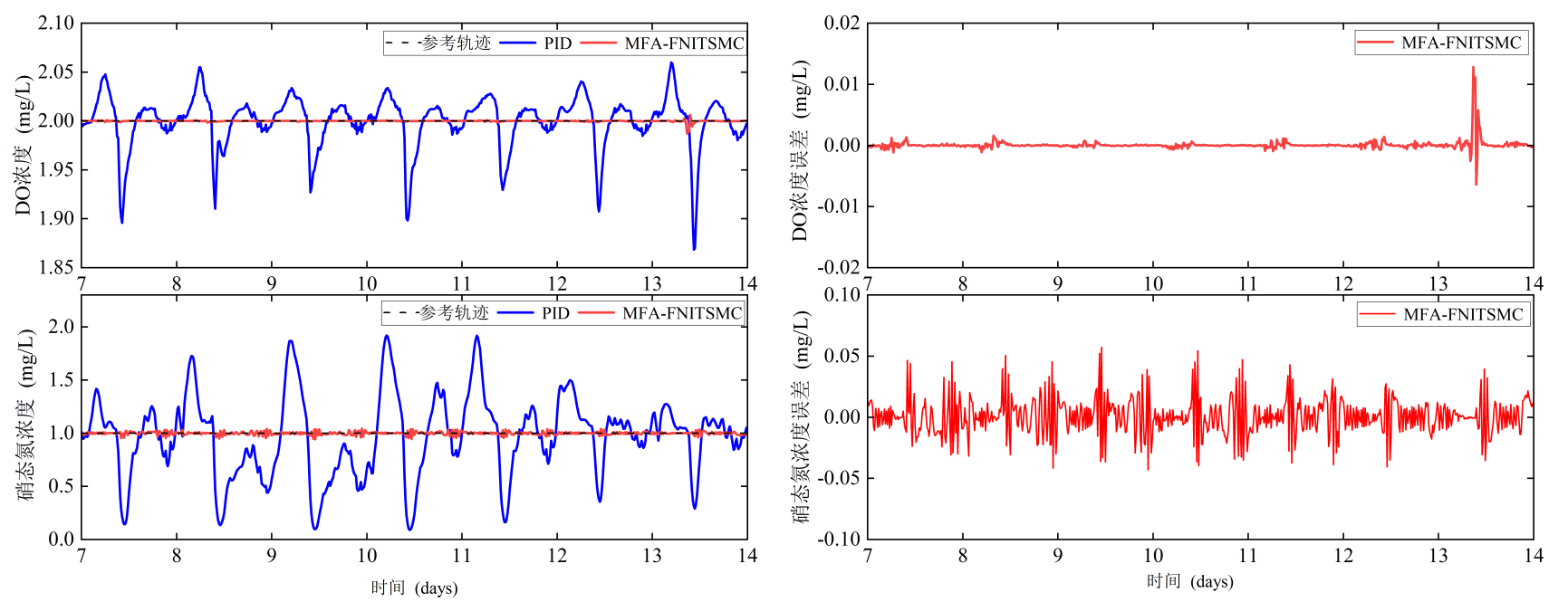
(a) 溶解氧和硝态氮浓度 (b) 溶解氧和硝态氮跟踪误差

图6 雨天溶解氧和硝态氮控制效果

表4 情况3中不同算法控制性能对比

上述三种情况下的实验结果表明，本文所提的MFA-NFITSMC控制方法在污水处理厂和的控制中具有良好的控制效果，与目前已有的控制方法相比，本文方法在ISE、IAE和三个指标中均优于其他方法，其控制精度更高，鲁棒性更强，能够有效抑制WWTP系统中的内部扰动和外部扰动。

综上所述，本文所提方法能够有效控制具有非线性、慢时变和强扰动特性的WWTP系统，与已有的方法相比，MFA-NFITSMC方法具有优越的动态性能和稳态性能，鲁棒性更强。

结论:

本文针对污水处理过程难以建立精确模型以及存在未知干扰的问题，提出了一种基于数据驱动的无模型自适应非奇异快速积分终端滑模控制方法。所提方法不需要WWTP精确的数学模型及先验知识，仅需实时I/O数据，其误差收敛快，控制律非奇异，具有全局鲁棒性。此外，通过理论分析证明了系统的误差收敛性和BIBO稳定性。三种情况下的仿真结果表明，与其他控制方法相比，本文提出的MFA-NFITSMC方法在WWTP系统的控制中具有更高的控制精度以及更强的鲁棒性，能够有效抑制未知干扰对WWTP系统的影响。此外，所提方法为一类非线性慢时变、模型难以建立的多工况复杂系统的跟踪控制问题提供了一种新的解决思路。

作者简介:

徐宝昌，中国石油大学（北京）信息科学与工程学院/人工智能学院，副教授，博士生导师。现为中国石油学会会员，中国化工学会会员。曾参与多项国家级、省部级科研课题的科研工作，并在国内外核心刊物发表了论文70余篇；其中被SCI、EI、ISTP收录30余篇。