论文题目：基于尺度不变正则化的快速混合时频域Radon变换多次波压制方法

录用期刊/会议：85th EAGE Annual Conference & Exhibition(EI检索会议)

原文DOI：10.3997/2214-4609.202410587

原文链接：https://doi.org/10.3997/2214-4609.202410587

录用/见刊时间：2024年6月10日

作者列表：

1） 张 程 中国石油大学（北京） 人工智能学院 博24

2） 薛亚茹 中国石油大学（北京） 人工智能学院 电子系教师

3） 冯璐瑜 中国石油大学（北京） 人工智能学院 博20

4） 王 昕 中国石油大学（北京） 人工智能学院 研22

5） 梁 琪 中国石油大学（北京） 人工智能学院 研21

摘要:

Radon变换的反演分辨率决定了其应用于多次波压制的效果。在本文中提出了一种快速混合时频域Radon变换方法。这种方法结合了非迭代高分辨率Radon变换和混合时频域方法，避免了重复的矩阵求逆计算，并提高了Radon模型的稀疏性。此外，我们修改了稀疏Radon变换的反演目标函数，用尺度不变的L₁/L₂正则化替换了传统的L₁正则化，后者通过元素的绝对值之和来衡量分辨率，而前者能够更准确地描述能量聚焦。合成数据和现场数据的算例表明，本文方法可以显著提高Radon域的分辨率，从而实现更好的多次波压制效果，并减少残余多次波和一次波损伤。

背景与动机：

Radon变换将地震数据沿特定积分路径转换到Radon域，将一次波和多次波映射到不同区域。然而，Radon变换是非正交的，通常被视为一个反演问题来解决。但通常它是不适定的。由于地震数据的有限孔径和离散采样，Radon域中的能量扩散也会导致一次波和多次波的混叠。稀疏反演可以获得类似于无限孔径速度数据集的解，并采用迭代加权最小二乘法（IRLS）实现高分辨率反演。在稀疏反演中，通常使用L₁范数作为正则化来促进稀疏性，但是该正则化方法存在欠缺。

设计与实现:

时不变的Radon变换可以看成是频域反演问题：

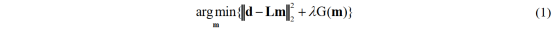
其中，在频率-偏移距（f-x）域中，d表示地震数据的时间-偏移距（t-x）域频率分量；而在频率-曲率（f-q）域中，m表示Radon域（τ-q域）模型，L是随频率变换的Radon变换正演模型算子，是非正交的。

为了更准确地衡量Radon系数的能量聚焦，本文用L₁/L_∞替换了L₁范数。然而，L₁/L_∞是非线性的，L_∞范数的值是元素绝对值的最大值。因此，将L₁/L_∞作为正则化项是难以最小化的。本文采用了加权矩阵方法：

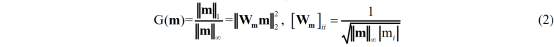
其中主频加权矩阵W_mf0由主频分量m_f0计算。由此得到主频约束反演形式：

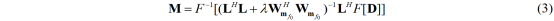
其中M是Radon域数据，D是时空域地震数据，F和F^-1分别代表傅里叶变换及其逆变换。

由于范数的等价性，L₂范数可以作为正则化中的等价项来简化求解，构建L₁/L₂。因此，我们可以根据交替方向乘子法（ADMM）采用稀疏信号恢复的尺度不变方法来解决以下问题：

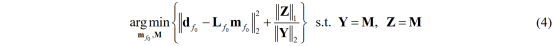
L_f0是在主频Radon算子，Y和Z是M的辅助变量。

本文方法(FMRTSIR)整体思路如下图所示：

图1 本文方法整体思路

实验结果及分析:

为了展示本文方法的效果，将本文方法应用于合成和现场地震数据集的多次波压制。所得到的结果与对比方法得到的结果进行了比较。

合成数据实验结果图例如图2和图3中所示。由图2，本文方法获得了比对比方法更稀疏的反演结果。多次波压制结果在图3中展示。本文方法的多次波残留少于对比方法。

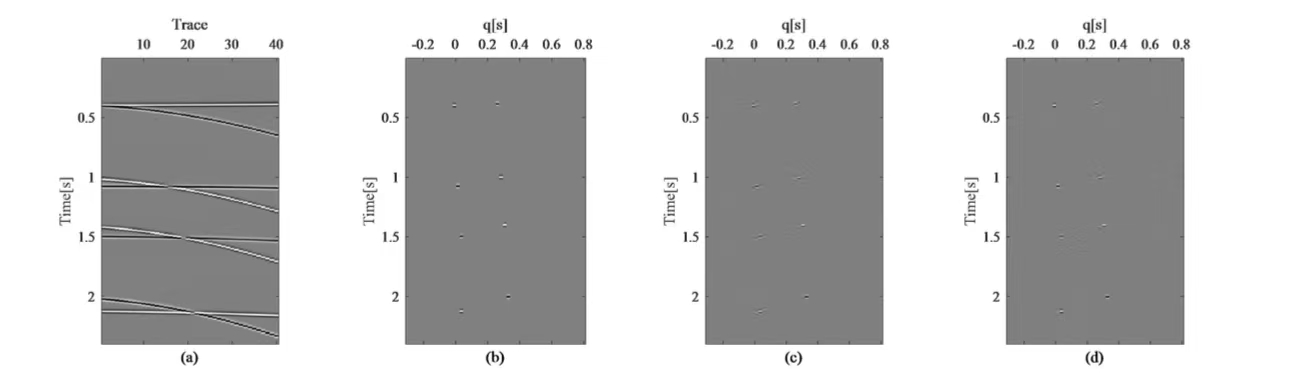
图2 合成数据示例

(a) 合成地震数据集； (b) 合成Radon域数据；

(c) 对比方法反演的Radon域数据； (d) 本文方法反演的Radon域数据

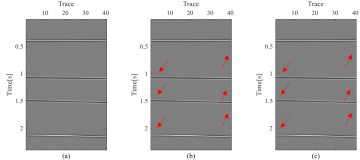
图3 合成数据的多次波压制

(a) 合成数据一次波； (b) 对比方法得到的一次波； (c) 本文方法得到的一次波

为了进一步证明本文方法的有效性，本文将其应用于实际数据，如图4和图5所示。图4(a)是经过动校正的CMP道集。图4(b)和4(c)分别是对比方法和本文方法得到的Radon模型，其中更稀疏的模型是由本文方法获得的。图5展示了近偏移距叠加的多次波压制结果。以图4(a)中显示的原始叠加部分为基准，本文方法在图4(c)中实现了更好的效果，与图4(b)中的对比方法相比。

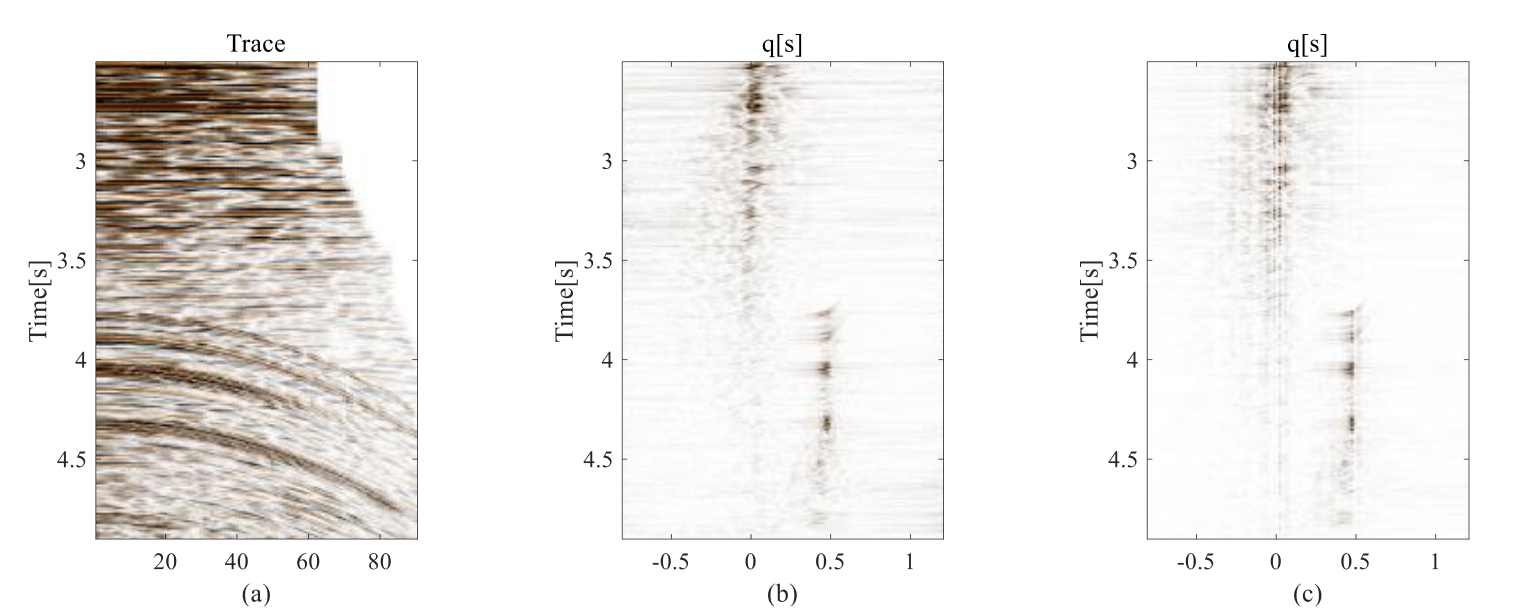
图4 实际数据示例

(a) CMP道集；(b) 对比方法反演的Radon域数据；(c) 本文方法反演的Radon域数据

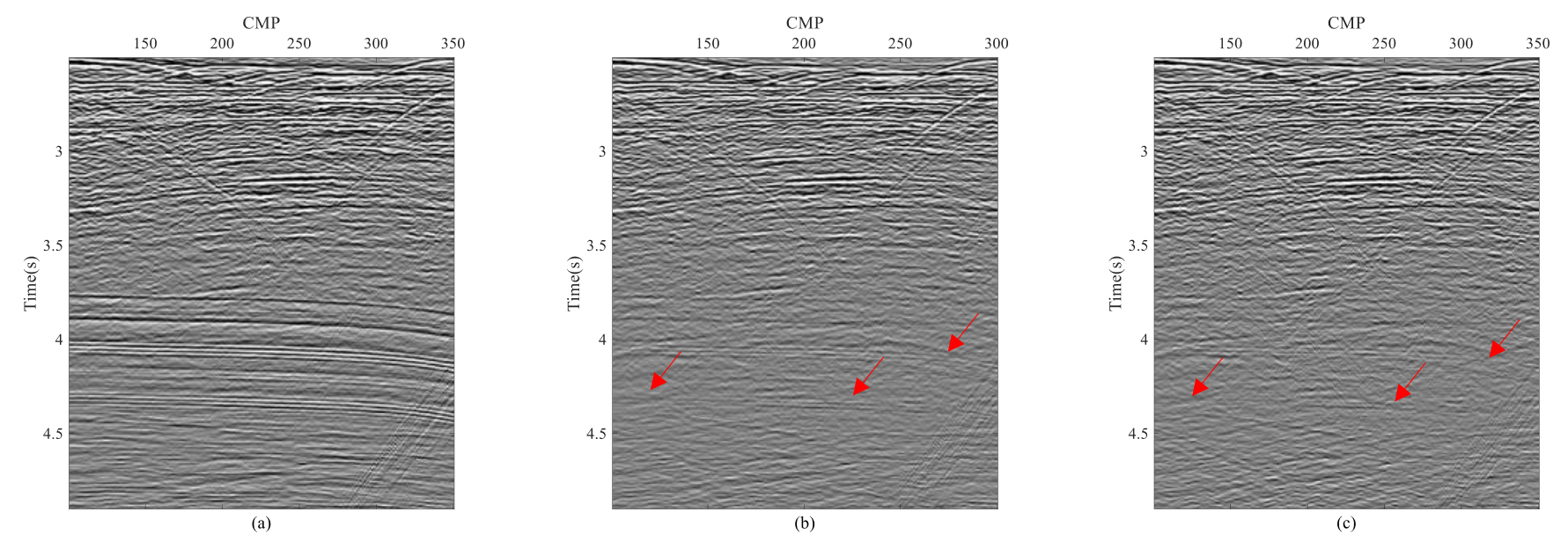
图5 实际数据的近偏移距叠加道集

(a)原始叠加道集；经(b)对比方法，(c)本文方法进行多次波压制

结论:

本文提出了一种快速混合时频域Radon变换反演方法，修改了Radon变换反演目标函数中的正则化项，用尺度不变正则化（SIR）替换了传统的L₁正则化，以增强能量聚焦。在合成数据和现场数据的例子中确认了所提出方法的更好效果。由数据实验得到验证，本文方法可以显著提高Radon模型的分辨率，从而改善多次波压制效果。

作者简介:

薛亚茹，副教授，博士生导师/硕士生导师。主要从事信号处理、图像处理、人工智能、地球物理反演等方面研究。