中文题目：基于平滑 MUSIC 的高分辨率方向性被动源面波频散谱成像方法

论文题目：High-resolution Directional Passive Surface Waves Dispersion Imaging Based on Smoothing MUSIC

录用期刊/会议：IEEE Geoscience and Remote Sensing Letters (中科院大类3区)

原文DOI：10.1109/LGRS.2024.3506165

录用/见刊时间：2024.11.20

作者列表：

1） 薛亚茹 中国石油大学（北京）人工智能学院 电子系教师

2） 梁   琪 中国石油大学（北京）人工智能学院 硕21

3） 曹静杰 自然资源部京津冀城市群地下空间智能探测与装备重点实验室

4） 姜   明 鹏城实验室

5） 冯璐瑜 中国石油大学（北京）人工智能学院 博20

6） 苏军利 中国石油大学（北京）人工智能学院 硕21

7） 张   程 中国石油大学（北京）人工智能学院 博24

摘要:

被动源面波频散成像广泛应用于浅地表横波速度反演中。然而，由于强方向性噪声源的存在导致频散谱往往偏离真实值。传统的波束形成方法能够校正频散谱，但分辨率有限。此外，实际记录包含随机噪声，会进一步降低了成像质量。为了解决频散谱成像分辨率较低及抗噪性问题，我们基于多重信号分类算法（MUSIC）及阵列空间平滑处理技术，提出了一种高分辨率的频散成像方法(SV-MUSIC)。首先，在MUSIC算法中引入速度变量来识别环境噪声的主导方位，提取稀疏的f-v谱。为进一步消除随机噪声的影响，对整个阵列进行划分及对空间相关矩阵进行平滑处理。模拟实验及现场试验证明了方法的有效性，能够在随机噪声条件下实现高分辨率的频散谱估计。

背景与动机:

近年来，在浅地表面波成像中，利用环境背景噪声（潮汐、微震或交通噪声）反演地层S波速度的面波方法引起了广泛的关注。与主动源面波成像方法不同，被动源面波成像方法易于部署，对环境友好，且能够提供更宽的低频信息反演更深层次的地质构造。该方法通常假设噪声源在空间上均匀分布，各方向振幅能量基本一致。然而，这一假设在实际环境中很难满足，使得经验格林函数出现不对称和虚假到时的情况，导致面波频散谱估计偏高。近年来，越来越多的学者关注在非均匀噪声源分布下提取准确频散谱。目前，大多数方法考虑常规的波束形成方法对频散谱进行方位校正，分辨率有限，且未考虑到随机噪声的干扰。

设计与实现:

本文提出了一种基于多重信号分类算法（MUSIC）与空间平滑处理技术的被动源面波频散成像方法，能够有效提高频散谱的分辨率，并且克服了基于MUSIC算法的频散成像方法在噪声情况下频散谱质量下降的问题。

基于常规的波束形成（倾斜叠加）的频散成像方法，如下式所示。

 

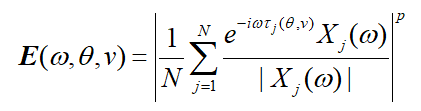
基于MUSIC算法频散成像方法，其大致流程如图1所示。首先构造频域的空间相关矩阵（SCM）。

 

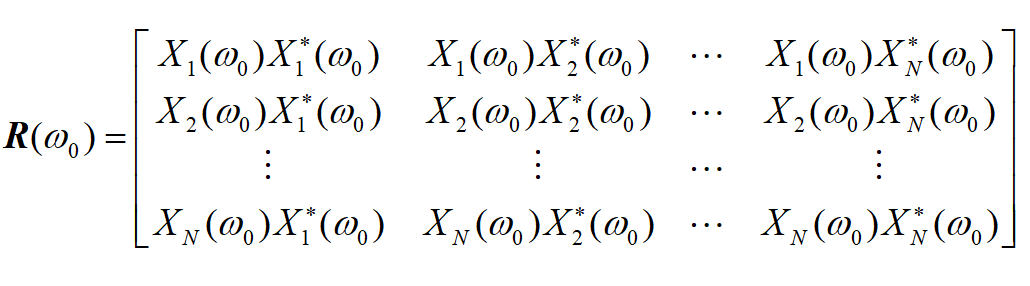
利用特征值分解，在不考虑随机噪声的情况下，根据特征值大小将SCM划分为面波信号子空间和零子空间。其中，面波信号子空间由第一个大特征向量构造，而零子空间则由其他较小的特征向量构造。利用零子空间与导向矢量的正交性，从而获得高分辨率的频率-方位-速度谱。

 

将上述的三维张量沿速度方向进行叠加，得到频率-方位谱。其中，谱峰值处对应的方位作为噪声源的主导方位。

 

在频率-方位-速度谱中沿主导方位切片提取主导方位下的频率-速度谱，形成最终的频散谱。

 

 

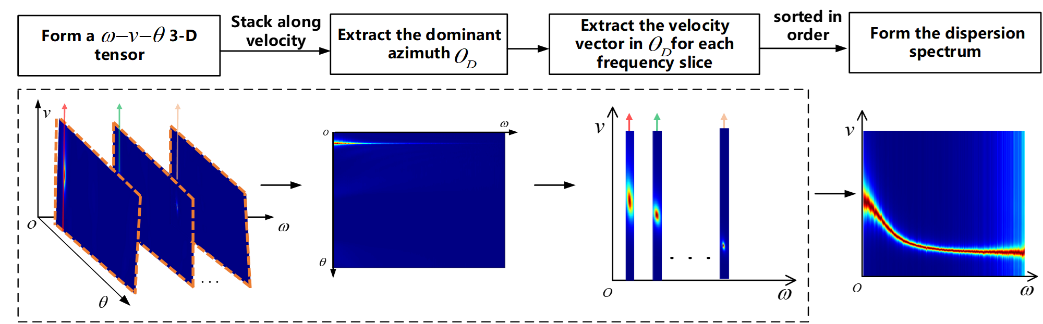
图1 基于MUSIC算法的频散成像基本流程

为了提高方法在噪声环境下的鲁棒性，本文设计了一种空间平滑方法来减轻噪声的影响。首先，确定优势方位角。随后，将L型阵列分解为两个垂直的线阵，并选择与主导方位更对齐的最优线阵，并构造相应的导向矢量。

 

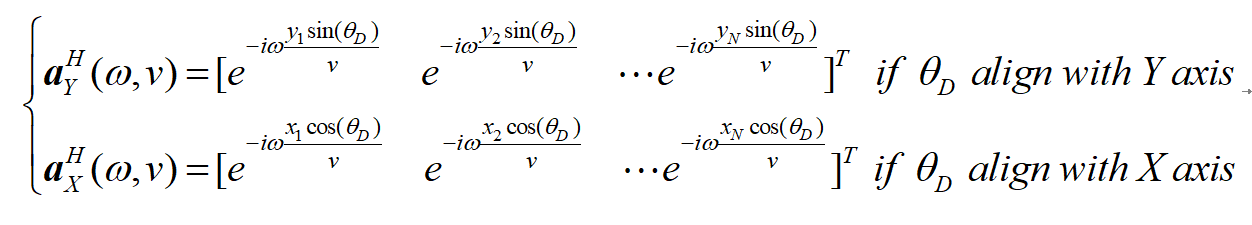
将线阵分成若干组，分别计算每组子阵列的空间相关矩阵，对所有子阵的空间相关矩阵取平均，得平滑后的空间相关矩阵：

  

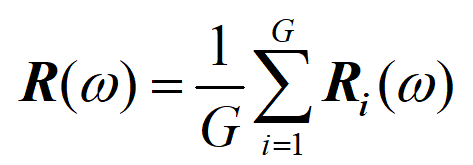
基于空间平滑的MUSIC算法频散成像方法，其方法流程如图2所示。

 

图2 基于SV-MUSIC方法频散成像基本流程

实验结果及分析:

我们依据理论的地层模型模拟面波频散特性，生成不同噪声源模型下的地震记录，并对比不同方法下形成的频率-方位谱与频散谱，其相应结果如图3、4、5所示。

A. 模拟数据-单/多主导噪声源模型

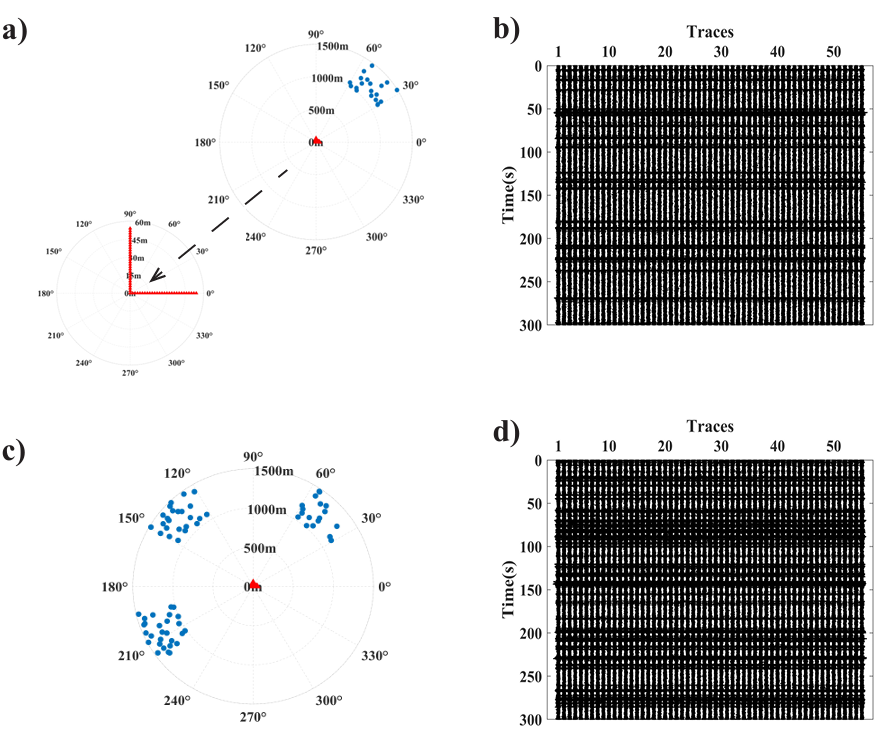
图3 方向性噪声源模型及合成记录

(a)和(b)单主导噪声模型和合成记录; (c)和(d)多主导噪声模型和合成记录

 

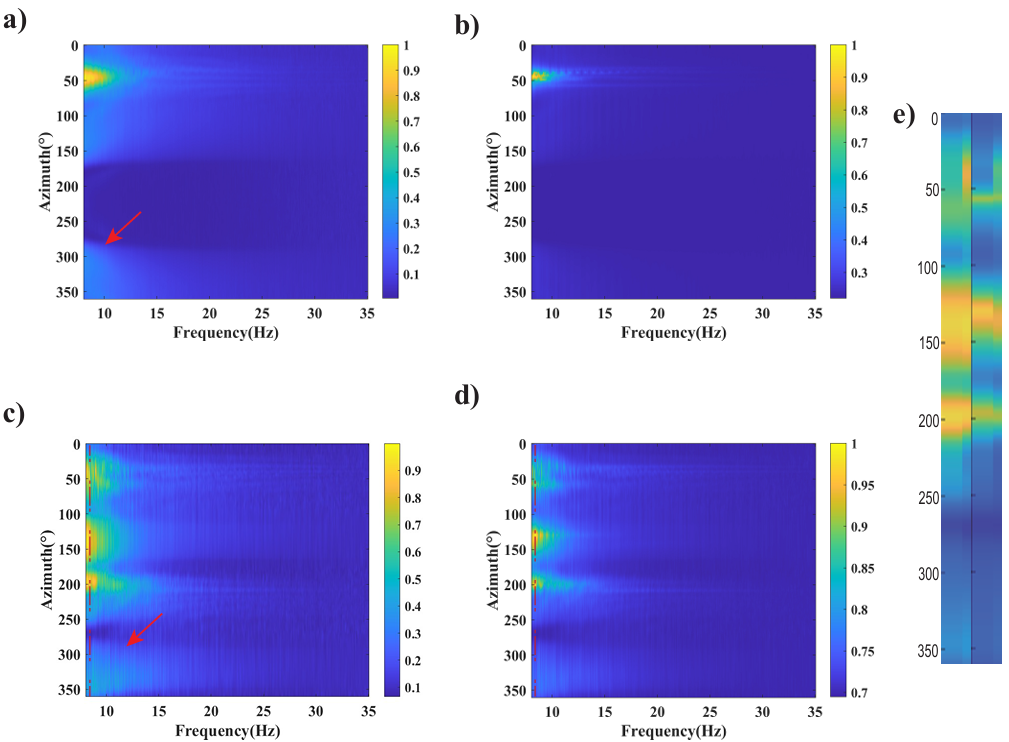
图4 频率-方位谱

(a)和(b)单主导噪声模型下的倾斜叠加与MUSIC方法下的结果;

(c)和(d)多主导噪声模型下的结果; (e)是在8Hz下从(c)和(d)中提取的方位谱对比

 

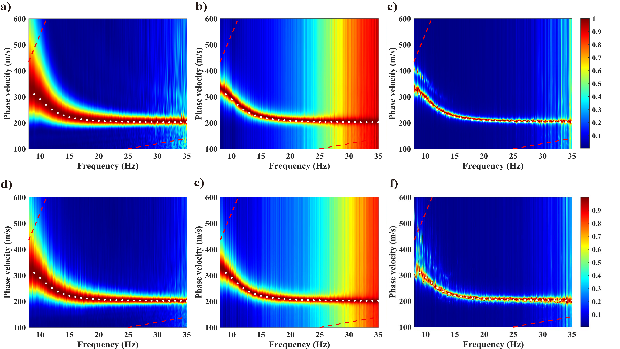
图5 方向性噪声模型下的频散谱

 (a)-(c)为倾斜叠加、MUSIC和SV-MUSIC形成的单主导噪声模型;

 (d)-(f)分别为多主导噪声模型下的结果 

为了进一步证明本文方法的有效性，我们将其应用于实际数据，试验地点及观测系统如图6（a）和图6（b）所示。图7为检波器所接收到的地震记录。图8和图9为实际数据下采用常规波束形成、传统MUSIC及SV-MUSIC方法得到的频率-方位谱与频散谱。

B. 实际数据

 

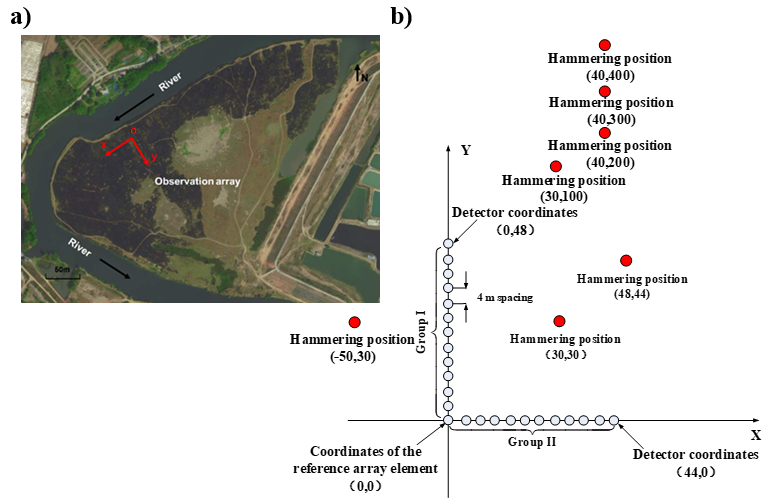
图6 现场试验

(a) 试验场地卫星图像; (b)观测系统和震源分布情况

  

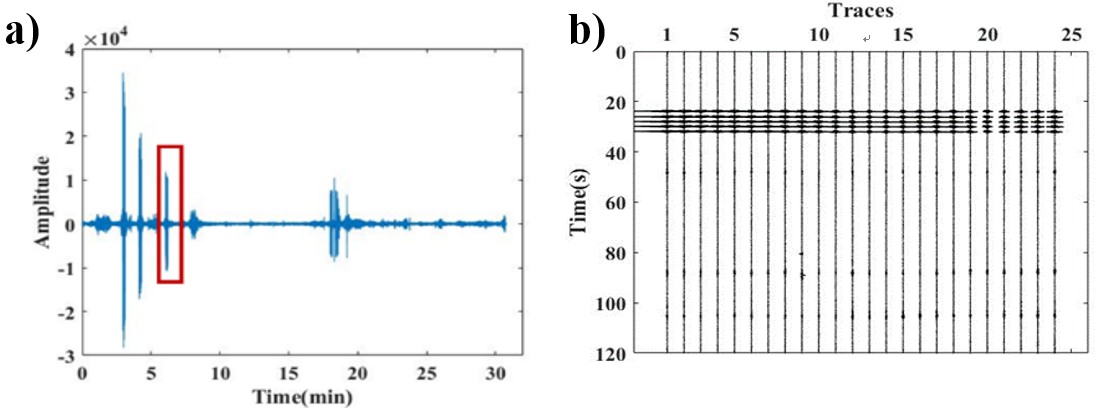
图7 实际地震数据

(a) 单个检波器记录; (b) 含有强方向噪声源的地震记录

 

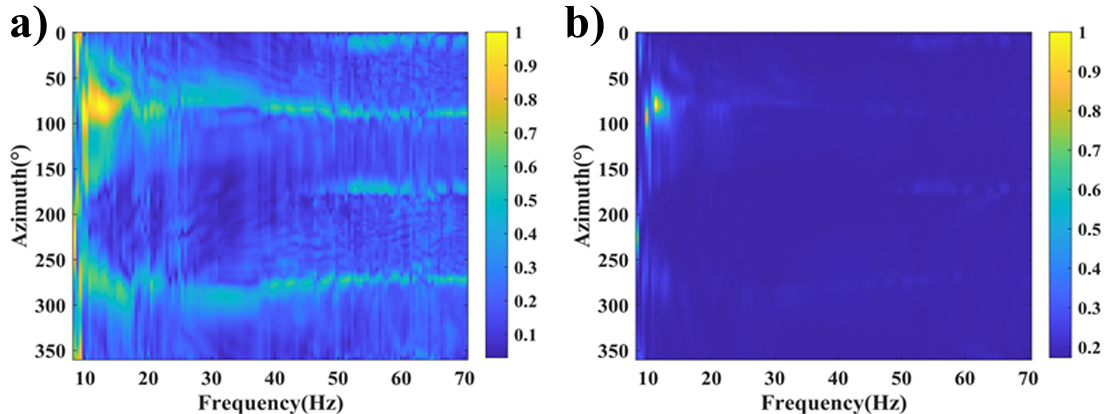
图8 频率-方位谱 

(a) 倾斜叠加法; (b) 基于MUSIC方法 

 

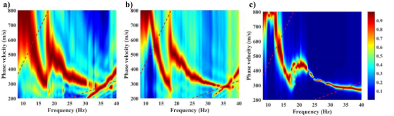
图9 实际数据下的频散谱

 (a) 倾斜叠加结果; (b) MUSIC结果; (c) SV-MUSIC结果

结论:

本文提出了基于空间平滑的SV-MUSIC被动源面波频散谱成像方法，该方法结合了MUSIC算法的高分辨率和常规波束形成方法的鲁棒性优点。通过合成数据验证了该方法的可行性，能够在不同的噪声模型下保持良好的性能；通过试验数据表明，该方法不仅能获得准确高分辨的频散谱，且有效地抑制随机噪声的干扰。

作者简介:

薛亚茹，副教授，博士生导师/硕士生导师。主要从事信号处理、图像处理、人工智能、地球物理反演等方面研究。