中文题目：SD-SSTA: 考虑偏斜分布的统计静态时序分析算法

论文题目：SD-SSTA: Statistical Static Time Analysis Algorithm Considering Skewed Distribution

录用期刊/会议：2024 International Symposium of Electronics Design Automation (ISEDA) (EI索引国际会议)

原文链接：https://www.ssslab.cn/assets/papers/2024-deng-SDSSTA.pdf 

DOI：10.1109/ISEDA62518.2024.10618081

录用/见刊时间：2024-3-26

作者列表：

1） 邓福星 中国石油大学（北京） 人工智能学院 硕 23

2） 冯一航 中国石油大学（北京） 人工智能学院 硕 23

3） 牛   丹 东南大学 自动化学院

4） 吴   枭 北京华大九天科技股份有限公司

5） 金   洲 中国石油大学（北京）人工智能学院

 

背景与动机:

静态时序分析 (Static Timing Analysis，STA) 是近年来在数字电路设计中应用最广泛和最成功的分析引擎之一。然而，确定性静态时序分析 (Deterministic Static Timing Analysis, DSTA)没有考虑工艺参数的波动对电路性能的影响，这引起了人们对确定性静态时序分析能否有效模拟统计变化的关注。因此，统计静态时序分析 (Statistical Static Timing Analysis，SSTA)已被提出并被广泛研究。传统的SSTA算法，如基于高斯分布的概率传播算法和蒙特卡罗算法，无法达到高精度和良好的性能。本文提出了一种考虑偏态分布的SSTA算法——SD-SSTA，该算法成功地实现了到达时间和时序宽裕量的精确计算，并且具有时间和空间上的优异性能。

设计与实现:

（1）算法框架

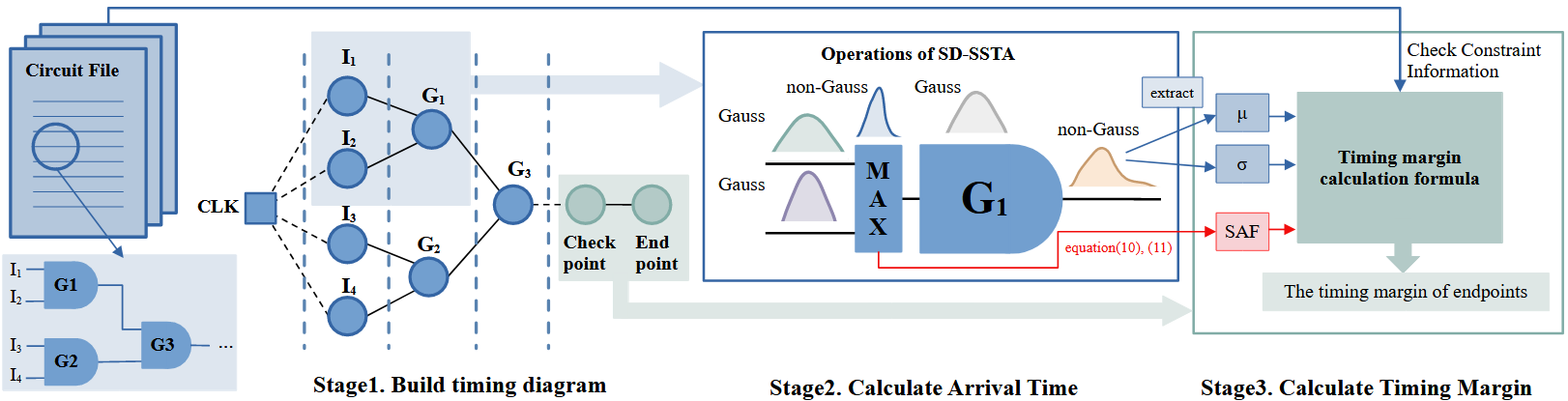
图1 SD-SSTA算法的实现过程

我们提出的SD-SSTA算法分为以下三个阶段。(1) 读取电路设计文件，建立时序图的数据结构。(2) 进行前向传播，从时序图的根节点开始逐步计算所有节点的到达时间。(3) 计算指定时序路径终点处的时序宽裕量。SD-SSTA算法流程如图1所示。

（2）构建时序图

我们收集电路的统计数据，组织电路设计文件，其中包括描述电路结构和时序信息的各个重要部分。图2 (a)是一个简单的电路示例，SD-SSTA算法通过读取电路设计文件构建如图2 (b)所示的时序图。

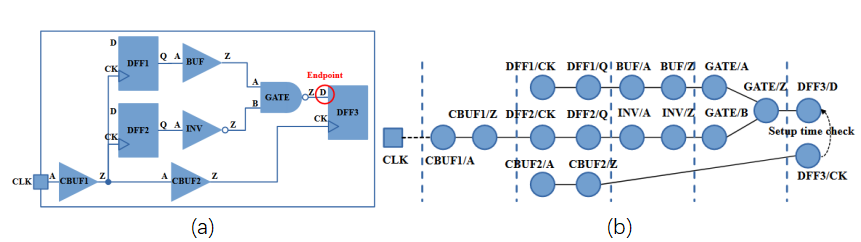
图2(a) 示例电路图，(b)对应的时序图

（3）SD-SSTA的操作

本文通过在高斯分布中加入偏度系数来描述非高斯分布。因此SD-SSTA算法的到达时间计算包括两个部分。

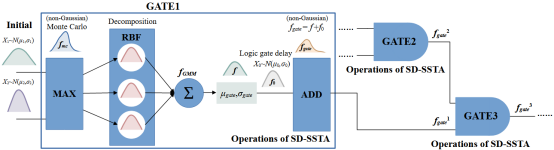
图3 非高斯分布的Max和Add操作的实现

 a. µ和σ: Max运算后通常形成非高斯分布。所以我们用高斯混合模型（Gaussian Mixture Model，GMM）建立模型最大值的概率密度函数（Probability Density Function，PDF）。首先利用蒙特卡罗模拟方法对非高斯分布进行建模，然后利用GMM进行拟合。换句话说，它可以分解成基本函数单元（Radial Basis Function，RBF)。进一步，我们从模型的属性中提取每个拟合RBF的µ和σ。因此，我们将非高斯分布作为公式(1)的线性组合来处理，如图3所示。最后，通过公式(2)提取到达时间µ和σ:

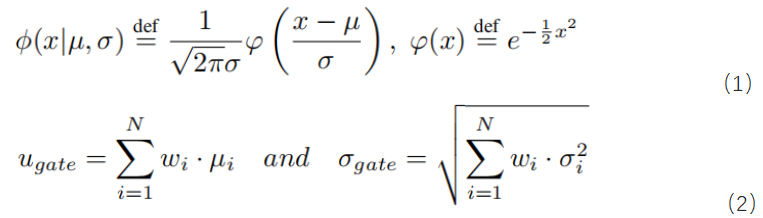
b.偏度系数: 两个相关高斯随机变量(X1和X2)的最大值的PDF形式为：

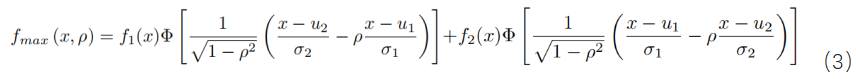
其中fi(x)分别是i = 1,2的高斯分布。

三阶矩是偏度的度量。因此，通过计算三阶矩，我们可以描述MAX运算后非高斯分布的偏度。计算公式如下：

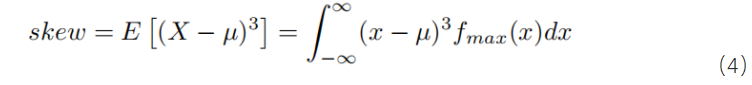
（4）计算时序宽裕量

SD-SSTA算法计算指定时序路径终点处的时序宽裕量。对于图2(a)中的上升沿触发的触发器，在DFF/D处下降信号的时序宽裕量应用以下公式进行计算。

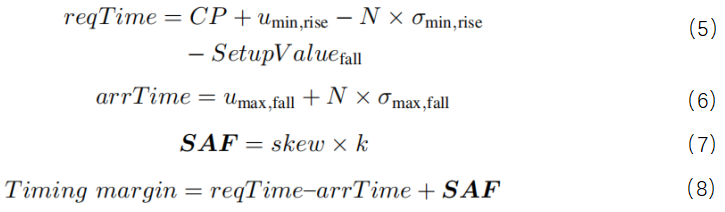
（5）性能优化

 图4 名称映射方法

在STA中，逻辑门的名称通常以字符串的形式存储在电路文件中。对于大规模的电路，字符串的搜索和比较将消耗大量的内存和时间。我们提出了一种名称映射方法，将电路文件中一个逻辑门的所有名称映射为整数，并且在程序运行过程中只使用整数进行计算。这种方式，特别是在大规模电路中，节省了大量的内存，也在一定程度上减少了运行时间。图4显示了Hash函数的映射过程。

实验结果及分析:

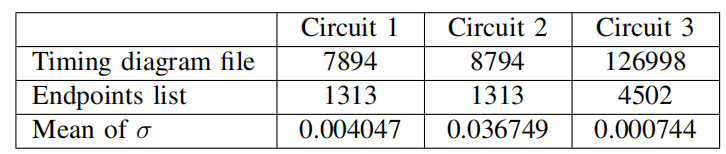
表1 关于测试用例的信息。（前两行反映了案例的数据大小：第一行的值可以反映时序图中的节点和边的数量；第二行的值表示端点的数量；第三行的值表示标准差的均值）。

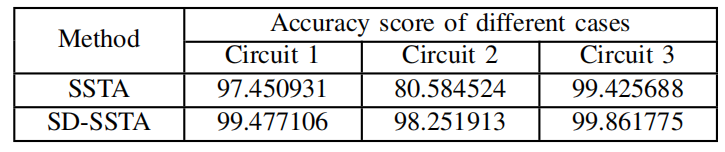
表2 每个样例的最终准确度得分 

根据评分公式计算出相应的时序宽裕量准确度得分。表2比较了三种不同测试用例下SSTA和SD-SSTA算法计算的时间宽裕量准确性。从表1中可以看出，电路3的方差小，即工艺参数的变化范围很小，因此传统算法可以实现精确的计算。而电路2的方差大，传统方法无法解决，SD-SSTA算法的优越性从而体现出来。

 

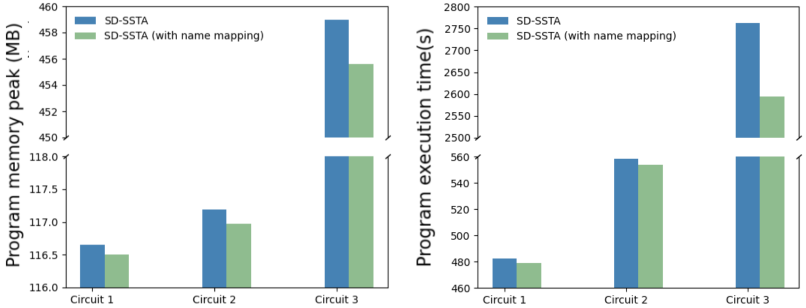
图5 使用名称映射方法前后的时间和内存比较

从图5可以看出，名称映射方法减少了算法的时间和内存，对大规模电路的效果尤为明显。

结论:

本文提出了一种基于非高斯分布的SSTA方法SD-SSTA。不同于传统的SSTA算法，我们利用GMM模型对非高斯分布进行建模，并在高斯分布的基础上引入偏度系数。非高斯分布用µ，σ和偏度系数表示，即非高斯分布被参数化。利用这些参数，准确地计算了到达时间的前向传播。在时间宽裕量的计算中，考虑了偏斜的影响，并在公式中引入了SAF。与传统的SSTA结果相比，SD-SSTA算法显著提高了时间宽裕量计算的准确度。此外，通过名称映射有效地减少了内存和时间，提高了算法的性能。

通讯作者简介:

金洲，副教授，中国石油大学（北京）计算机系副教授，入选北京市科协青年人才托举工程、校青年拔尖人才。主要从事集成电路设计自动化（EDA）方面的研究工作。主持并参与国家自然科学基金青年项目、培育项目、重点项目，科技部重点研发微纳电子专项、高性能计算专项青年科学家项目，国家重点实验室开放课题、企业横向课题等。在DAC、TCAD、TODAES、SC、PPoPP、IPDPS、TCAS-II、ASP-DAC等重要国际会议和期刊上发表60余篇高水平学术论文。获EDA2青年科技奖、SC23最佳论文奖、ISEDA23荣誉论文奖、IEEJ九州支部长奖等。

 联系方式：jinzhou@cup.edu.cn