一类非线性离散系统基于非线性滤波器的鲁棒自适应控制方法
中文题目:一类非线性离散系统基于非线性滤波器的鲁棒自适应控制方法
论文题目:A novel nonlinear filter-based robust adaptive control method for a class of nonlinear discrete-time systems
录用期刊/会议:processes (JCR Q2)
原文DOI:https://doi.org/10.3390/pr12010171
原文链接:https://www.mdpi.com/2227-9717/12/1/171
录用/见刊时间:2024.1.11
作者列表:
1)赵泽一 中国石油大学(北京)信息科学与工程学院/人工智能学院 计算机科学与技术 本21
2)王 珠 中国石油大学(北京)信息科学与工程学院/人工智能学院 自动化系教师
3)王 倩 中国石油大学(北京)信息科学与工程学院/人工智能学院 控制科学与工程 硕21
摘要:
本文介绍了一种利用非线性滤波器的创新自适应控制方法对于非线性离散时间系统的特定子集,考虑输入和输出噪声。该系统可以转换为非线性自回归移动平均外源输入(NARMAX)模型。将离散Nussbaum增益的概念引入解决与未知前馈或控制方向相关的理论约束增益,并且引入了扩展的自适应调谐序列以促进参数更新。在无噪声的情况下,渐近输出跟踪和全局稳定性是通过自适应控制实现。此外,在存在输入噪声和输出噪声的情况下设计了一种新颖的非线性滤波器来产生更准确的滤波输出,这提高了控制系统准确适应和跟踪的能力。最后,提供了示例来展示方法的有效性和准确性。
背景与动机:
近年来,人们对连续非线性系统的自适应控制进行了大量的研究。许多工业过程表现出非线性行为,并且已经开发了各种用于识别非线性系统的方法,这些方法可以应用于输入非线性系统,输出非线性系统以及输入和输出非线性的系统。这一努力需要对后退设计方法进行深入的研究,扩大其范围以满足非线性连续时间系统的需要。这种系统可以有效地转换为输出反馈形式或参数严格反馈形式。这些调查的结果也被扩展到包含连续多输入多输出(MIMO)系统的领域。尽管在理解连续系统中的自适应控制方面取得了相当大的进步,但值得注意的是,这些发现的离散对应物还没有得到相应的探索。
设计与实现:
1、无干扰自适应控制设计
考虑如下输入前馈输出反馈形式的非线性SISO离散时间系统:
 (1)
(1)
其中,
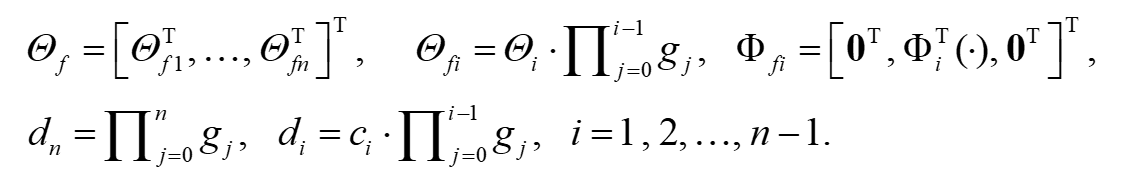 (2)
(2)
在无噪声情况下,即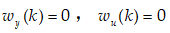 ,考虑自适应控制方案。在不存在输入噪声和输出噪声的情况下,将式(2)中的所有方程迭代代入合并,可以得到如下系统方程:
,考虑自适应控制方案。在不存在输入噪声和输出噪声的情况下,将式(2)中的所有方程迭代代入合并,可以得到如下系统方程:
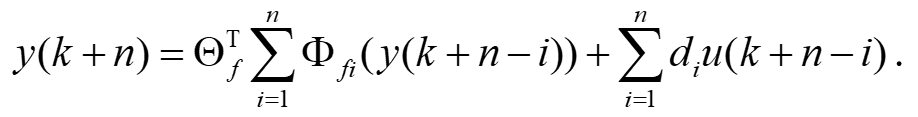 (3)
(3)
产生的残差可以用下式表示,
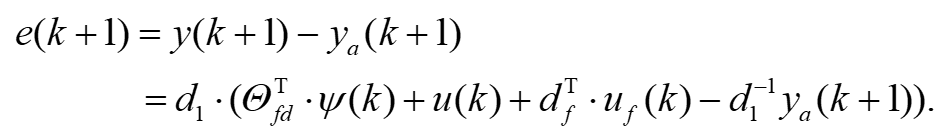 (4)
(4)
在式(4)中,存在未知的前馈增益d1,使得在不知道d1的情况下递归参数估计具有挑战性,并且确定参数估计的更新方向是一个挑战。
因此,为了解决这一限制,引入了离散Nussbaum增益。离散Nussbaum增益N(p(k))可以表示为
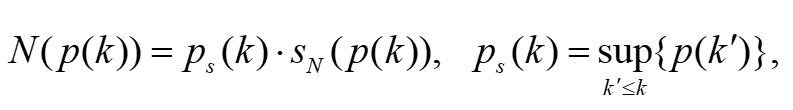 (5)
(5)
通过将离散Nussbaum增益引入参数估计,我们得到如下更新规律:
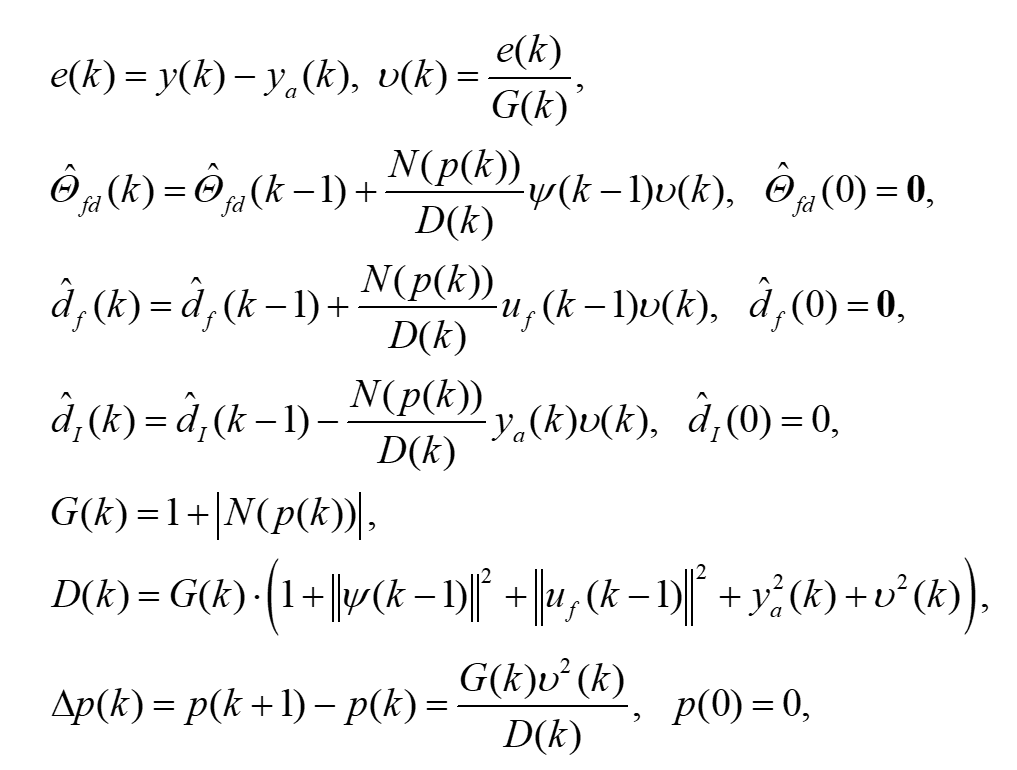 (6)
(6)
其中u(k)为增广误差,D(k)为归一化序列。根据p(k),确定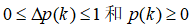
因此,序列p(k)很好满足。
为了加快参数更新过程,采用了一个修正的自适应调谐因子来更新律。基于非递减非负序列p(k),可将调谐因子描述为
![]() (7)
(7)
通过引入扩展自适应调谐因子,可以将式(6)中的参数更新过程修改为:
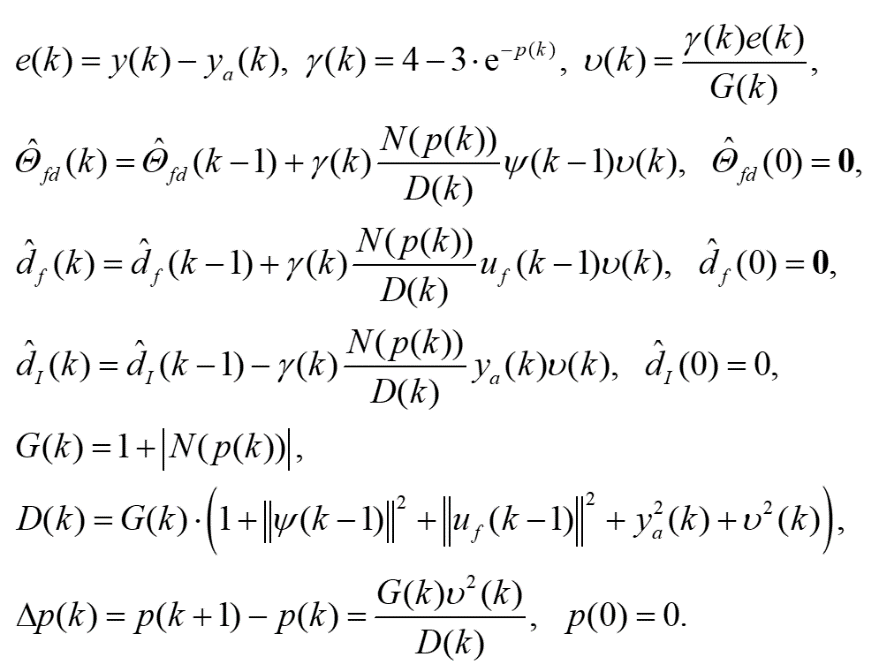 (8)
(8)
2、 一种基于非线性滤波的扰动自适应控制方法
针对存在输入噪声和输出噪声的非线性离散系统,提出了一种新颖的非线性滤波器,即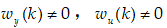
通过这种非线性滤波器,可以得到更精确的滤波输出。基于卡尔曼滤波方程理论,研究了非线性系统状态估计的有效估计技术。根据卡尔曼滤波器,时间更新和测量更新方程也可以推广到非线性滤波器中,在存在噪声的情况下作为状态观测器,设计了一个非线性滤波器。
非线性滤波器的时间更新方程为:
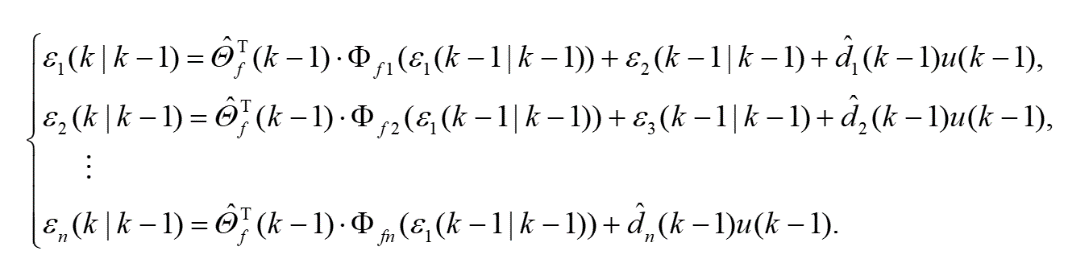 (9)
(9)
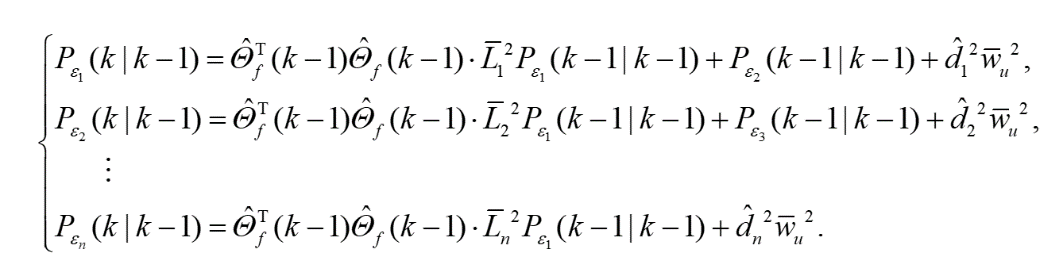 (10)
(10)
非线性滤波器的测量更新方程为:
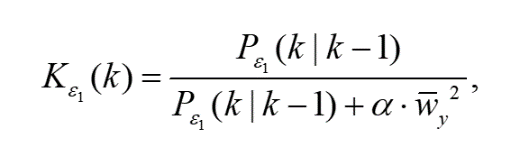 (11)
(11)
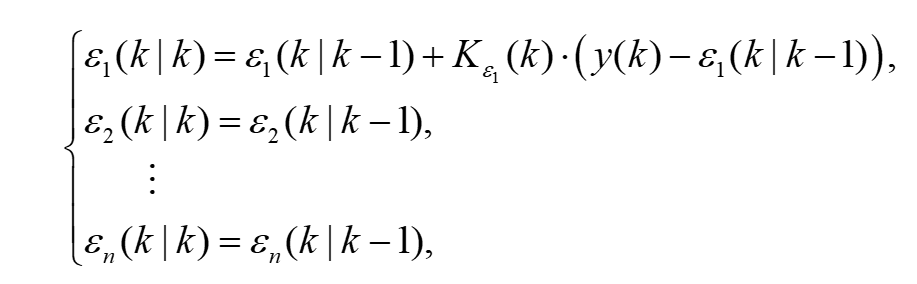 (12)
(12)
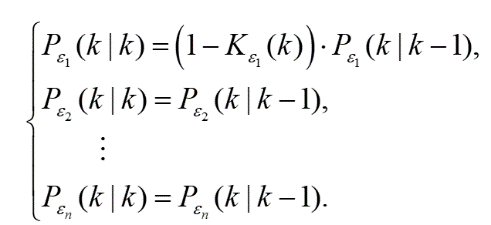 (13)
(13)
根据参考文献中自适应因子的设计,α项可取为
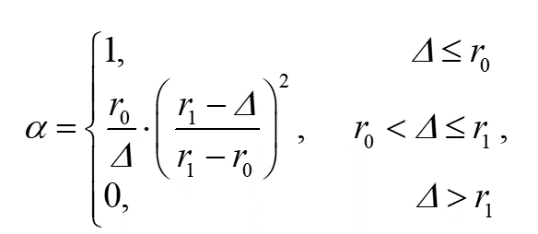 (14)
(14)
为了获得更精确的滤波输出,期望能够跟踪参考轨迹,将非线性滤波器的输出设置为第一滤波子系统状态。在历元k处的滤波输出描述为
![]() (15)
(15)
为了发展滤波输出的自适应控制,我们定义
![]()
必须修改递归参数更新律(6)。使用参考文献中的死区方法,使用项l(k)来设置更新过程的阈值。因此,利用滤波后的输出,参数更新规律如下:
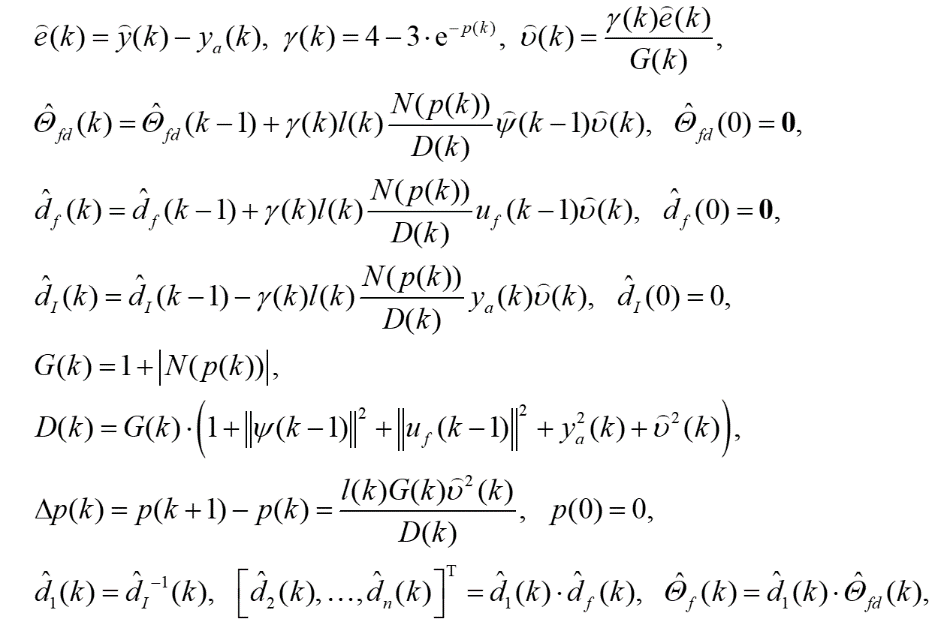 (16)
(16)
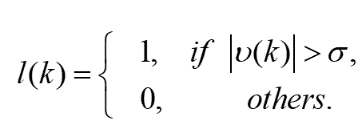
利用式(9)-(14)中的非线性滤波算法,并应用具有参数更新律的自适应控制,给出了一种完整的基于非线性滤波的鲁棒自适应控制方法。
实验结果及分析:
例1:考虑以下无噪声二阶离散非线性系统
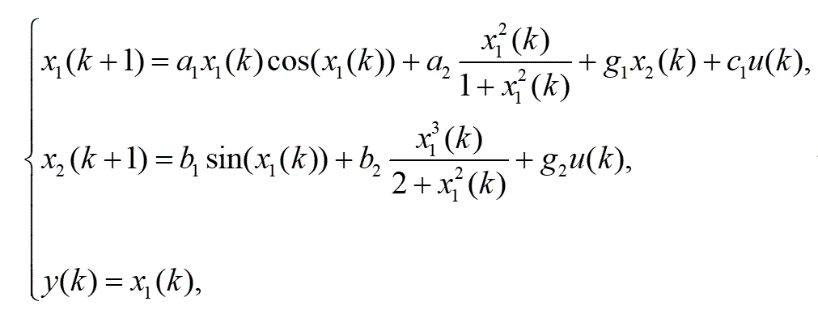
采用具有递归参数更新律的一般自适应控制,进行了两次仿真,证明控制系统的自适应性不受与第一子系统状态相关的前馈增益方向c1变化的影响。因此,第一次假定c1项为负值。然后,在模拟系统的第二次运行中假设为正c1。结果如图1-3所示。图1不仅显示了输出和参考的比较,还显示了跟踪误差和基准0的比较。很明显,无论是负增益还是正增益c1,自适应方法在无噪声情况下都是有效的。控件输入的有界性如图2所示。最后,离散Nussbaum增益N(x(k))如图3所示。很容易看出,离散努斯鲍姆增益在两个方向上搜索以检测参数更新方向。
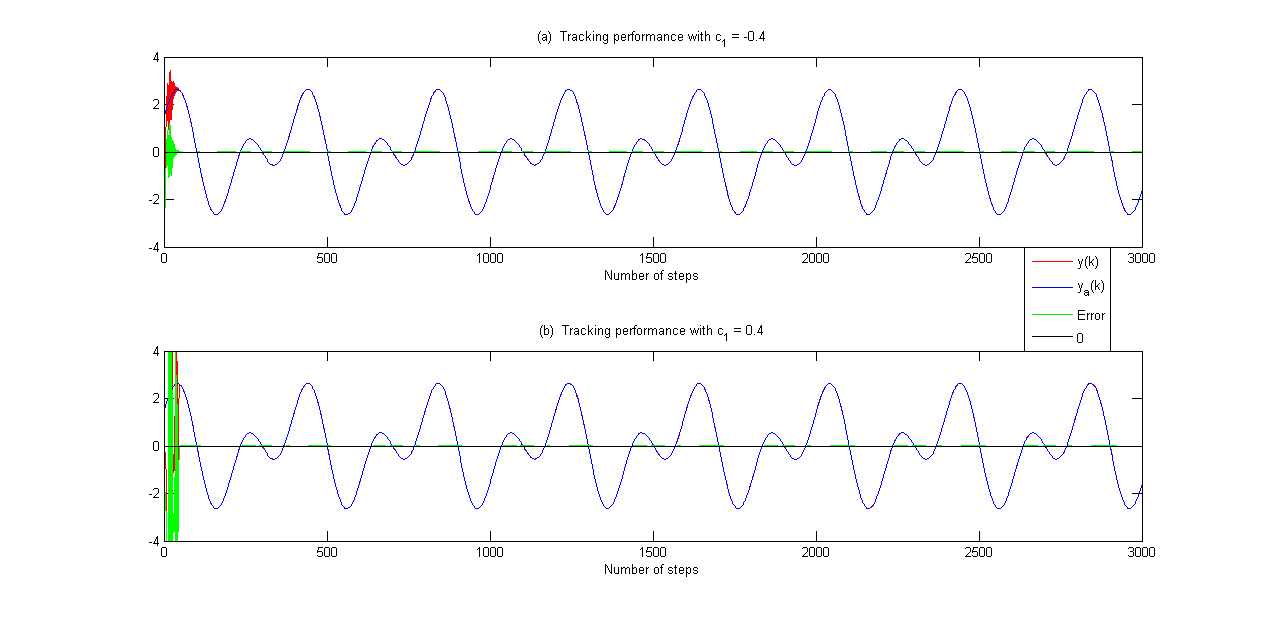
图1 例1的追踪表现比较
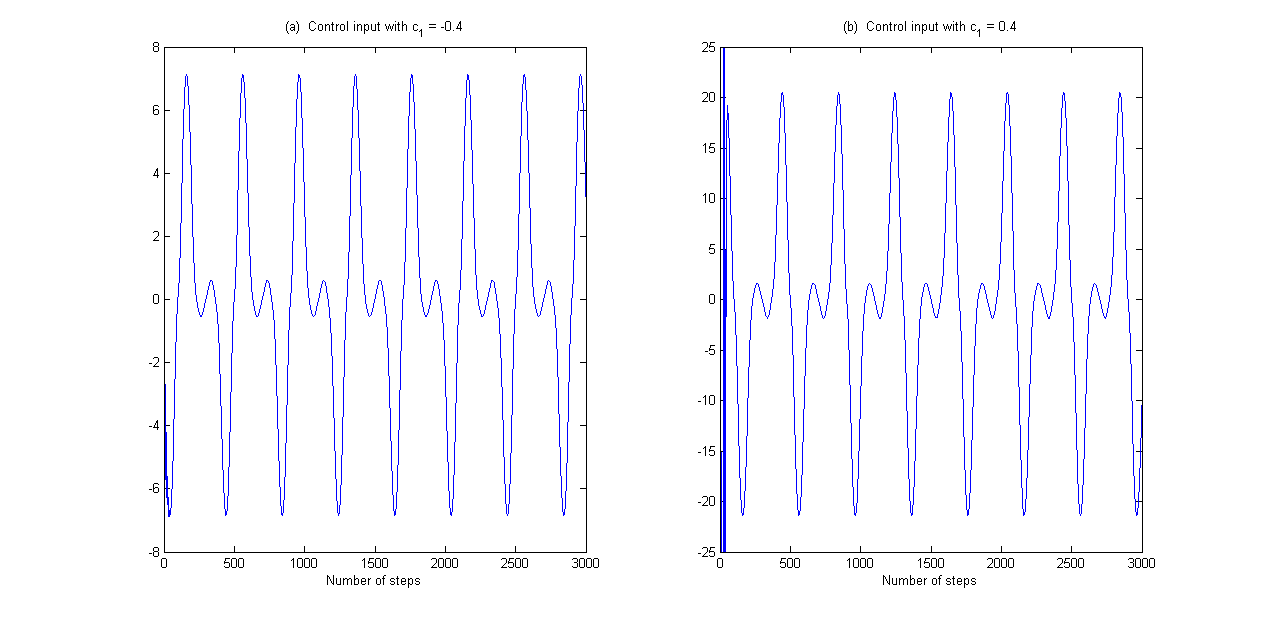
图2 例1的输入控制
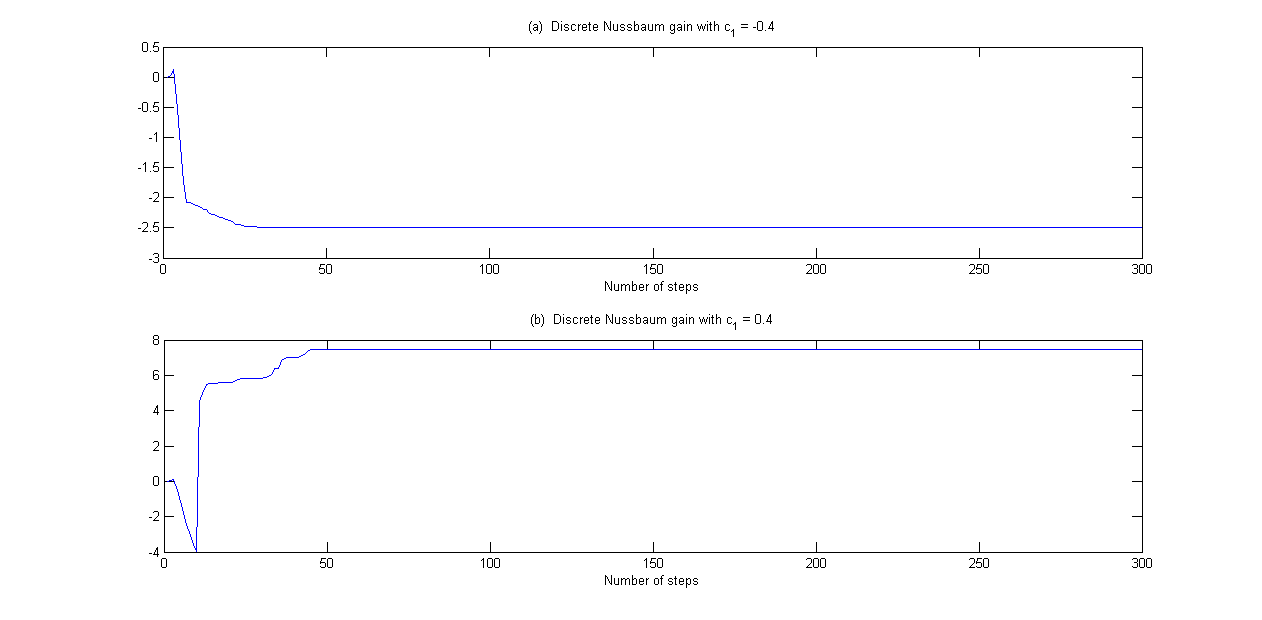
图3 例1中的Nussbaum 增益N(x(k))
例2:在存在输入噪声和输出噪声的情况下,考虑一个类似的离散非线性系统:
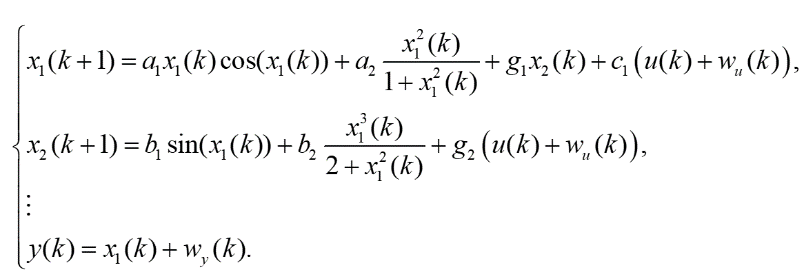
输入和输出噪声满足,
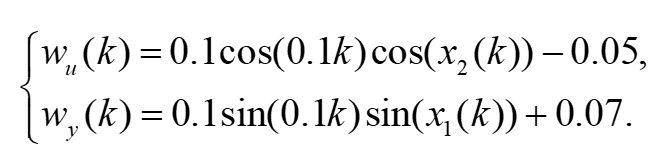
初始状态和期望的参考轨迹与例1中相同。采用式(9)-式(14)中的非线性滤波方法,并采用递归参数更新律和自适应控制,可以得到滤波后输出的跟踪性能。需要注意的是,扩展的自适应调谐序列和阈值分别取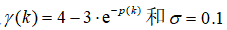
此外,还将所提出的非线性滤波器的结果与使用通用自适应方法提供的结果进行了比较。比较结果如图4-6所示。图 4 显示了跟踪性能的比较。输入有界性和离散Nussbaum增益分别如图5和图6所示。
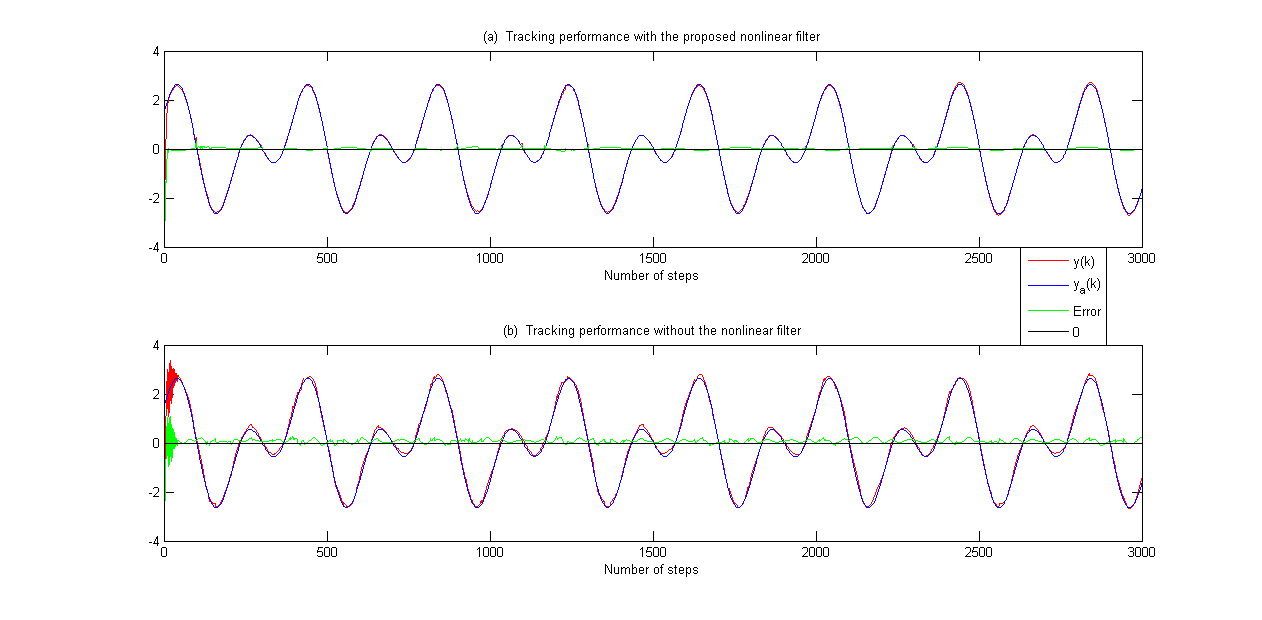
图4 例2的追踪表现比较
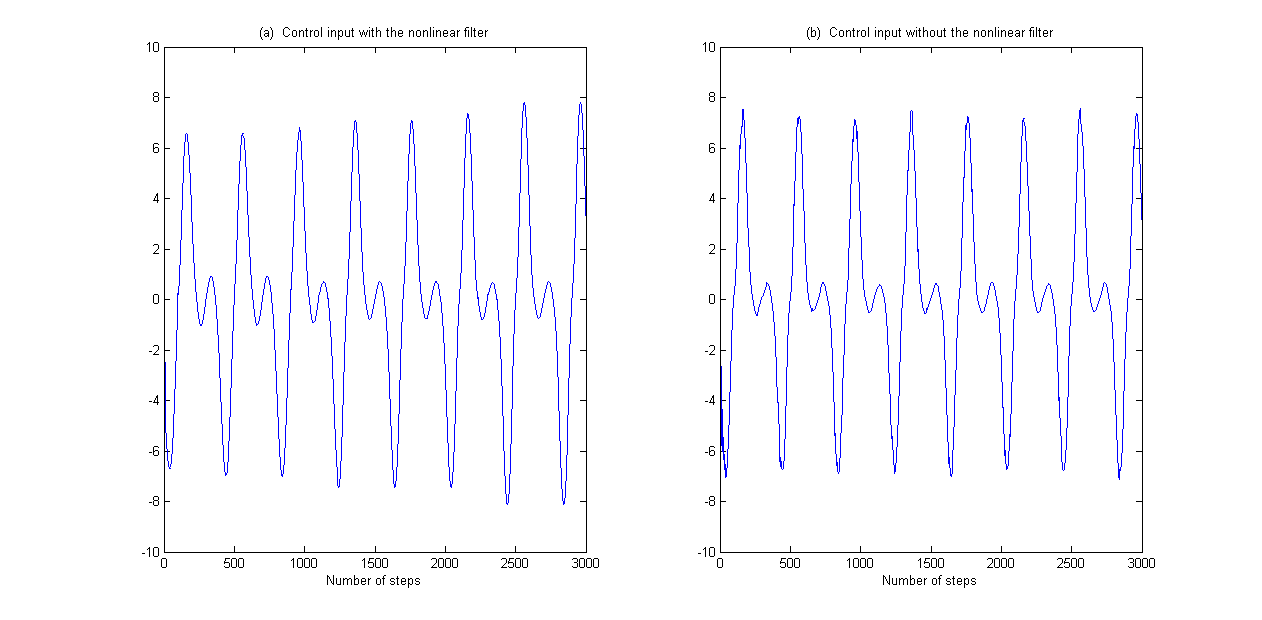
图5 例2的输入控制
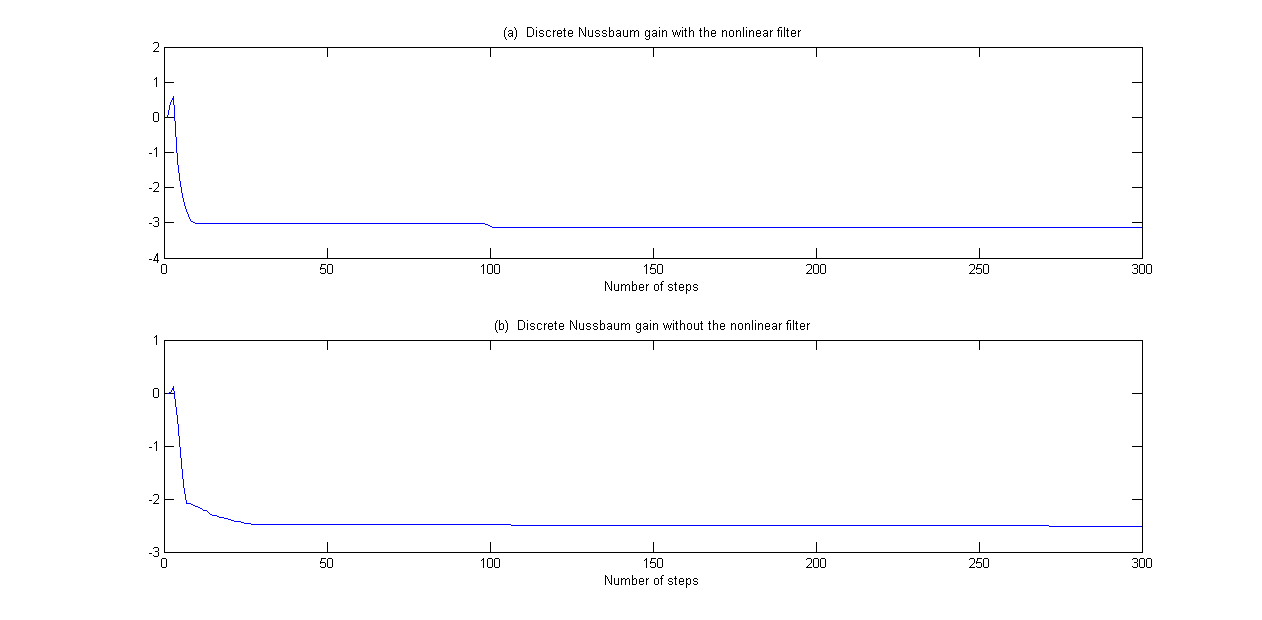
图6 例2中的Nussbaum 增益N(x(k))
例3:考虑正项c1=0.4的情况。在与例2相同的输入噪声和输出噪声存在的情况下,仿真模型和所有其他系统参数也与例2相同。初始状态和期望的参考轨迹与例1相同。通过使用非线性滤波器和相应的自适应控制方案,可以得到滤波后输出的跟踪性能;阈值设为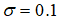
与例2类似,不同自适应控制方案的对比结果如图7-9所示。跟踪性能的比较如图7所示。
此外,图8说明了输入有界性的结果。图9描述了离散Nussbaum增益的比较。从例2、例3和图4-9中,我们可以得出以下结论:
1.无论c1 > 0还是c1 < 0,基于非线性滤波器的自适应控制方法都能比一般自适应控制方案更准确地显示跟踪性能;
2. 为了跟踪参考轨迹,采用基于非线性滤波器的自适应控制方法实现了小超调量和短沉降时间;
3. 在所有比较示例中,控制输入都是有界的;
4. 所提出的识别算法采用离散Nussbaum增益,可以设计成在两个方向内检测模型参数的方向。
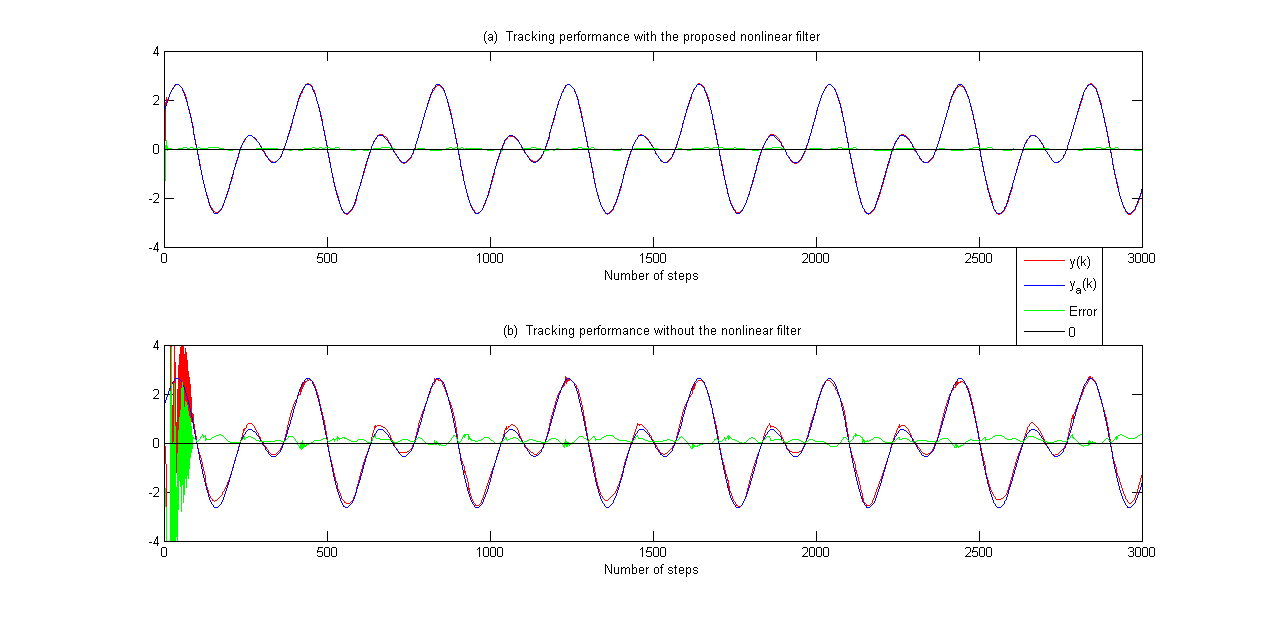
图7 例3的追踪表现比较
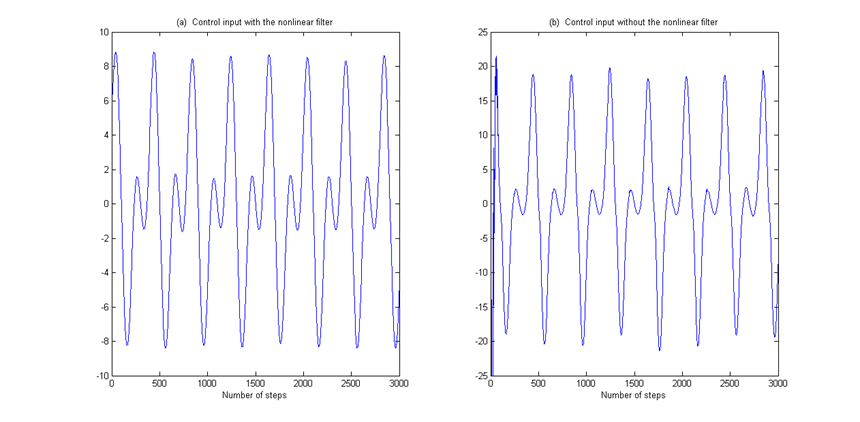
图8 例3的输入控制

图9 例3中的Nussbaum 增益N(x(k))
结论:
本文提出了一种新的基于非线性滤波器的自适应控制方法,并将其引入到一类具有输入和输出噪声的非线性离散系统中。该方法结合了输入前馈和输出反馈。为了解决确定参数估计更新方向的问题,利用离散努斯鲍姆增益,以及扩展的自适应调谐序列来加快更新的过程。该方法同样适用于无噪声系统,并证明了无噪声系统的收敛性。在存在输入和输出噪声干扰的情况下,受卡尔曼滤波方程的启发,将时间更新和测量更新方程推广到非线性滤波器中,并证明了算法的收敛性。与一般不加滤波的自适应控制方法相比,该方法在识别过程中随参数模型的变化呈现自适应的控制率变化。它提供了更好的参数轨迹跟踪和实时性。相比之下,传统的辨识方法保持固定的控制率,不随估计参数的变化而变化。基于非线性滤波器的自适应控制提供了更精确的滤波输出和更好的参考轨迹跟踪。仿真结果验证了理论结果。该方法可应用于工程实践,实现对此类非线性系统的鲁棒自适应控制。
通讯作者简介:
王珠,男,博士,中共党员,现任中国石油大学(北京)副教授、硕士生导师。2016年至今在中国石油大学(北京)自动化系工作,现任北京人工智能学会理事、中国化工学会信息技术应用专业委员会青年委员。长期从事系统辨识与智能控制、石化过程故障预警、工艺优化以及基于深度学习的时间序列预测等方面的研究工作,以第一作者或通讯作者身份发表高水平学术论文20余篇。主持国家自然科学基金项目及多个重点企业横向项目。

